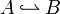Notations
From LLWiki
Contents |
Logical systems
For a given logical system such as MLL (for multiplicative linear logic), we consider the following variations:
| Notation | Meaning | Connectives |
|---|---|---|
| MLL | propositional without units | 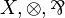
|
| MLLu | propositional with units only | 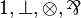
|
| MLL0 | propositional with units and variables | 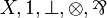
|
| MLL1 | first-order without units | 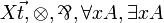
|
| MLL01 | first-order with units | 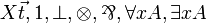
|
| MLL2 | second-order propositional without units | 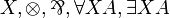
|
| MLL02 | second-order propositional with units | 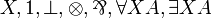
|
| MLL12 | first-order and second-order without units | 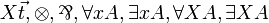
|
| MLL012 | first-order and second-order with units | 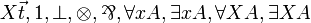
|
Formulas and proof trees
Formulas
- First order quantification:
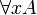 with substitution A[t / x]
with substitution A[t / x]
- Second order quantification:
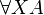 with substitution A[B / X]
with substitution A[B / X]
- Quantification of arbitrary order (mainly first or second):
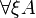 with substitution A[τ / ξ]
with substitution A[τ / ξ]
Rule names
Name of the connective, followed by some additional information if required, followed by "L" for a left rule or "R" for a right rule. This is for a two-sided system, "R" is implicit for one-sided systems.
For example: 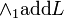 .
.
Semantics
Coherent spaces
- Web of the space X:
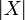
- Coherence relation of the space X: large
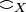 and strict
and strict 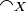
Finiteness spaces
- Web of the finiteness space
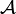 :
: 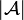
- Finiteness structure of the space
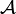 :
: 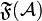 (we use \mathfrak, which is consistent with the fact that
(we use \mathfrak, which is consistent with the fact that 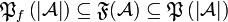 ).
).
Nets
- The free ports of a net R: fp(R).
- The result of the connection of two nets R and R', given the partial bijection
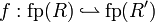 :
: 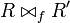 .
.
- The number of loops in the resulting net:
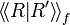 (includes the loops already present in R and R').
(includes the loops already present in R and R').
Miscellaneous
- Isomorphism:
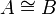
- injection:
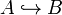
- partial injection: