Isomorphism
From LLWiki
This page is a stub and needs more content.
Two formulas A and B are isomorphic (denoted 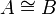 ), when there are two proofs π of
), when there are two proofs π of 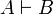 and ρ of
and ρ of 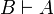 such that eliminating the cut on A in
such that eliminating the cut on A in
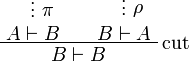
leads to an η-expansion of
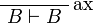 ,
,
and eliminating the cut on B in
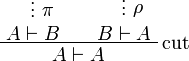
leads to an η-expansion of
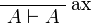 .
.
Linear logic admits many isomorphisms, but it is not known wether all of them have been discovered or not.