A formal account of nets
The aim of this page is to provide a common framework for describing linear logic proof nets, interaction nets, multiport interaction nets, and the likes, while factoring out most of the tedious, uninteresting details (clearly not the fanciest page of LLWiki).
Contents |
Preliminaries
The short story
- the general flavor is that of multiport interaction nets;
- the top/down or passive/active orientation of cells is related with the distinction between premisses and conclusions of rules, (and in that sense, a cut is not a logical rule, but the focus of interaction between two rules);
- cuts are thus wires rather than cells/links: this fits with the intuition of GoI, but not with the most common presentations of proof nets;
- because the notion of subnet is not trivial in multiport interaction nets, and to avoid the use of geometric conditions (boxes must not overlap but can be nested), we introduce boxes as particular cells;
- when representing proof nets, we introduce axioms explicitly as cells, so that axiom-cuts do not vanish.
Nets
Wires
A wiring is the data of a finite set P of ports
and of a partition W of P by pairs (the wires):
if 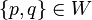 , we write W(p) = q and W(q) = p.
Hence a wiring is equivalently given by
an involutive permutation W of finite domain P,
without fixpoints (forall p,
, we write W(p) = q and W(q) = p.
Hence a wiring is equivalently given by
an involutive permutation W of finite domain P,
without fixpoints (forall p, 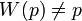 ): the wires are then
the orbits.
Another equivalent presentation is to consider W as
a (simple, loopless, undirected) graph, with vertices in P,
all of degree 1.
): the wires are then
the orbits.
Another equivalent presentation is to consider W as
a (simple, loopless, undirected) graph, with vertices in P,
all of degree 1.
We say two wirings are disjoint when their sets of ports are.
A connection between two disjoint wirings W and W' is
a partial injection 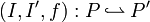 :
: 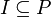 ,
,
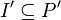 and f is a bijection
and f is a bijection 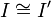 .
We then write
.
We then write 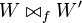 for the wiring obtained
by identifying the ports pairwise mapped by f, and then
``straightening`` the paths thus obtained to recover wires:
notice this might also introduce loops and we write
for the wiring obtained
by identifying the ports pairwise mapped by f, and then
``straightening`` the paths thus obtained to recover wires:
notice this might also introduce loops and we write 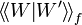 for the number of loops thus appeared.
for the number of loops thus appeared.
We describe these operations a bit more formally.
Write 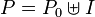 and
and 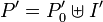 .
Then consider the graph
.
Then consider the graph 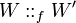 with vertices in
with vertices in
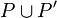 , and such that
there is an edge between p and q iff
q = W(p) or
q = W'(p) or
q = f(p) or
p = f(q):
in other words,
, and such that
there is an edge between p and q iff
q = W(p) or
q = W'(p) or
q = f(p) or
p = f(q):
in other words, 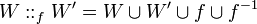 .
Vertices in
.
Vertices in 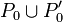 are of degree 1, and the others are of degree 2.
Hence maximal paths in
are of degree 1, and the others are of degree 2.
Hence maximal paths in 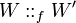 are of two kinds:
are of two kinds:
- straight paths, with both ends in
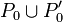 ;
;
- cycles, with vertices all in
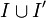 .
.
Then the wires in 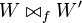 are the pairs {p,p'} such that
p and p' are the ends of a path in
are the pairs {p,p'} such that
p and p' are the ends of a path in 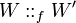 .
And
.
And 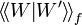 is the number of
cycles in
is the number of
cycles in 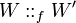 , or more precisely
the number of support sets of cycles (i.e. we forget about the starting
vertice of cycles).
, or more precisely
the number of support sets of cycles (i.e. we forget about the starting
vertice of cycles).
Lemma
Consider three wirings (P,W), (P',W') and (P'',W''),
and two connections 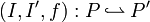 and
and
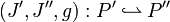 such that
such that 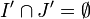 .
Then
.
Then
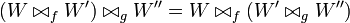
and
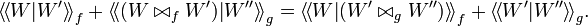
Proof.
The first equation holds because open maximal paths in
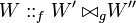 correspond with those in
correspond with those in
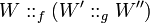 , hence in
, hence in
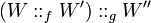 , hence in
, hence in
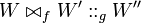 .
The second equation holds because both sides are two possible writings for
the number of loops in
.
The second equation holds because both sides are two possible writings for
the number of loops in 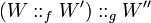
Nets
A signature is the data of a set
Σ of symbols, together with arity functions
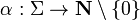 (number of
active ports, or conclusions)
and
(number of
active ports, or conclusions)
and 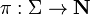 (number of
passive ports, or hypotheses).
In the remaining, we assume
such a signature is given.
(number of
passive ports, or hypotheses).
In the remaining, we assume
such a signature is given.
A cell c with ports in P is the data of
a symbol 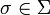 and of two disjoint lists
of pairwise distinct ports:
and of two disjoint lists
of pairwise distinct ports:
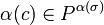 is the list of active ports
and
is the list of active ports
and 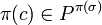 is the list of passive ports.
is the list of passive ports.
A net is the data of a wiring (P,W), of a set C of disjoint cells on
P, and of a number 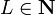 (the number of loops). It follows
from the definitions that each port
(the number of loops). It follows
from the definitions that each port 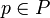 appears in exactly one wire and in
at most one cell: we say p is free if it is not part of a cell, and
p is internal otherwise. Moreover, we say p is dangling if
p is free and W(p) is internal. We write fp(R) for the set of
free ports of a net R.
appears in exactly one wire and in
at most one cell: we say p is free if it is not part of a cell, and
p is internal otherwise. Moreover, we say p is dangling if
p is free and W(p) is internal. We write fp(R) for the set of
free ports of a net R.
Generally, the “names” of internal ports of a net are not relevant, but free
ports matter most often: internal ports are the analogue of bound variables in
λ-terms.
More formally, an isomorphism from net R to net R'
is the data of a bijection of ports 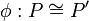 and a bijection
of cells
and a bijection
of cells 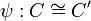 such that:
such that:
- for all
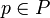 , W'(φ(p)) = φ(W(p));
, W'(φ(p)) = φ(W(p));
- for all
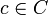 :
:
- σψ(c) = σc,
- for all
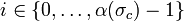 , α(ψ(c))i = φ(α(c)i),
, α(ψ(c))i = φ(α(c)i),
- for all
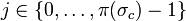 , π(ψ(c))j = φ(π(c)j);
, π(ψ(c))j = φ(π(c)j);
- L = L'.
Observe that under these conditions ψ is uniquely induced by φ.
We say that the isomorphism φ is nominal if moreover 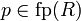 implies p = φ(p).
implies p = φ(p).
Subnets
We say two nets are disjoint when their sets of ports are.
Let R and R' be disjoint nets, and (I,I',f) be a
connection between W and W', such that
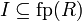 and
and 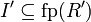 .
We then write
.
We then write 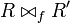 for the net
with wiring
for the net
with wiring 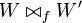 , cells
, cells
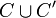 and loops
and loops 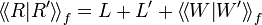 .
We say this connection is orthogonal if
.
We say this connection is orthogonal if 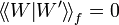 , and it is
modular if the ports in
, and it is
modular if the ports in 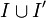 are all dangling: a modular connection is
always orthogonal.
are all dangling: a modular connection is
always orthogonal.
We say R0 is a subnet of R, if there exists a net R' and a connection
(I,I',f) between R0 and R' such that 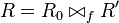 .
.
Lemma
Let R0, R1 and R' be nets such that R0 and R1
are disjoint from R,
(I,I',f) be a connection 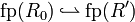 and φ an isomorphism
and φ an isomorphism 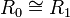 such that
φ(p) = φ(p') for all
such that
φ(p) = φ(p') for all 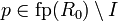 .
Then
.
Then 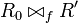 is nominally isomorphic to
is nominally isomorphic to
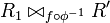 .
.
Rewriting
A net rewriting rule is a pair (r0,r1) of nets such that fp(r0) = fp(r1). Then an instance of this rule is a pair (R0,R1) such that there exist:
- nets R'0 and R'1 isomorphic to r0 and r1 respectively, namely R'i = φi(ri), so that moreover φ0(p) = φ1(p) for all
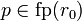 (in particular, fp(R'0) = fp(R'1));
(in particular, fp(R'0) = fp(R'1));
- a net R'', disjoint from R'0 and R'1;
- a connection
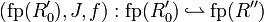 ;
;
such that each Ri is nominally isomorphic to
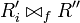 .
.
Typing
A typing system on signature Σ is the data of a
set Θ of types, an involutive negation 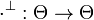 ,
together with a typing discipline for each symbol, i.e. a relation
,
together with a typing discipline for each symbol, i.e. a relation
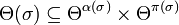 .
We then write
.
We then write 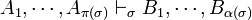 for
for 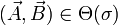 .
.
Then a typing for net R = (P,W,C) is a function 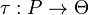 such that:
such that:
- for all
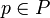 ,
, 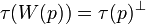 ;
;
- for all
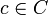 of symbol σ,
of symbol σ, 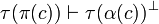 ;
;
where, in the last formula, we implicitly generalized
τ to lists of ports and 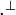 to lists of formulas,
in the obvious, componentwise fashion.
The interface of the typed net (R,τ) is then
the restriction of τ to fp(R).
to lists of formulas,
in the obvious, componentwise fashion.
The interface of the typed net (R,τ) is then
the restriction of τ to fp(R).
The idea, is that a wire {p,q} bears the type τ(q) (resp. τ(p)) in
the direction (p,q) (resp. (q,p)), so that a rule
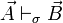 reads as an inference from passive inputs (hypotheses)
to active outputs (conclusions).
reads as an inference from passive inputs (hypotheses)
to active outputs (conclusions).
Observe that if (R,τ) is a typed net, and
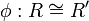 is an isomorphism,
then R' is typed and its interface is
is an isomorphism,
then R' is typed and its interface is 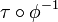 :
in particular, if φ is nominal, R' and R have the same interface.
:
in particular, if φ is nominal, R' and R have the same interface.
Now let (R,τ) and (R',τ') be typed nets
and (I,I',f) a connection so that 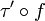 and
and
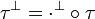 coincide on I.
Then this induces a typing of
coincide on I.
Then this induces a typing of 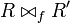 preserving the interface on the remaining free ports.
preserving the interface on the remaining free ports.
Boxes
A signature with boxes is the data of a signature Σ, together
with a box arity β(σ) for all symbol
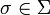 .
.
Then a net on signature with boxes (Σ,β) is the same as a net R on Σ plus, for each cell c of R, the data β(c) of a β(σc)-tuple of nets (with boxes) with free ports the internal ports of c.