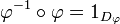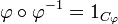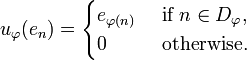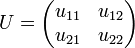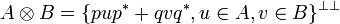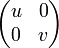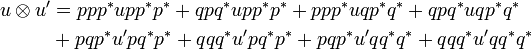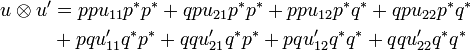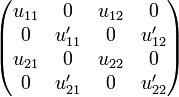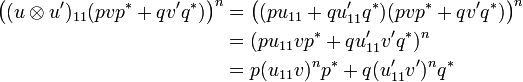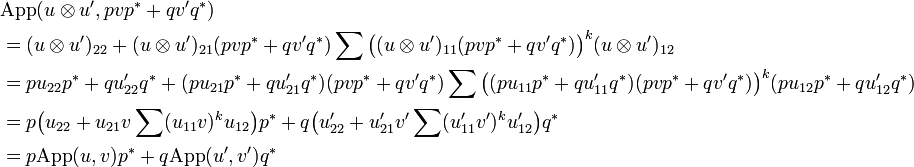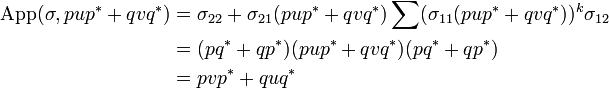Geometry of interaction
m (→The Geometry of Interaction as operators: remark on types : 0 belongs to any type) |
(→The tensor rule: warning on notation) |
||
| Line 241: | Line 241: | ||
\end{align}</math> |
\end{align}</math> |
||
| − | To understand this formula it is convenient to think <math>u</math> and <math>u'</math> as the internalizations of the matrices: |
+ | Once again the notation is motivated by linear logic syntax and is contradictory with linear algebra practice since what we denote by <math>u\tens u'</math> actually is the internalization of the direct sum <math>u\oplus u'</math>. |
| − | : <math>U = \begin{pmatrix}u_{11} & u_{12}\\ |
+ | |
| − | u_{21} & u_{22} |
+ | Indeed if we think of <math>u</math> and <math>u'</math> as the internalizations of the matrices: |
| − | \end{pmatrix} |
+ | : <math> |
| − | </math> and <math>U' = \begin{pmatrix}u'_{11} & u'_{12}\\ |
+ | \begin{pmatrix}u_{11} & u_{12}\\ |
| − | u'_{21} & u'_{22} |
+ | u_{21} & u_{22} |
| − | \end{pmatrix}</math> |
+ | \end{pmatrix} |
| − | so that we may write: |
+ | </math> and <math> |
| + | \begin{pmatrix}u'_{11} & u'_{12}\\ |
||
| + | u'_{21} & u'_{22} |
||
| + | \end{pmatrix}</math> |
||
| + | then we may write: |
||
: <math>\begin{align} |
: <math>\begin{align} |
||
u\tens u' &= ppu_{11}p^*p^* + qpu_{21}p^*p^* + ppu_{12}p^*q^* + qpu_{22}p^*q^*\\ |
u\tens u' &= ppu_{11}p^*p^* + qpu_{21}p^*p^* + ppu_{12}p^*q^* + qpu_{22}p^*q^*\\ |
||
| Line 256: | Line 256: | ||
Thus the components of <math>u\tens u'</math> are given by: |
Thus the components of <math>u\tens u'</math> are given by: |
||
: <math>(u\tens u')_{ij} = pu_{ij}p^* + qu'_{ij}q^*</math>. |
: <math>(u\tens u')_{ij} = pu_{ij}p^* + qu'_{ij}q^*</math>. |
||
| − | + | and we see that <math>u\tens u'</math> is actually the internalization of the matrix: |
|
| − | and we see that <math>u\tens u'</math> is actually the internalization of the matrix <math>U\tens U'</math> given by: |
||
| − | |||
: <math> |
: <math> |
||
| − | U\tens U' = |
+ | \begin{pmatrix} |
| − | \begin{pmatrix} |
+ | u_{11} & 0 & u_{12} & 0 \\ |
| − | u_{11} & 0 & u_{12} & 0 \\ |
+ | 0 & u'_{11} & 0 & u'_{12} \\ |
| − | 0 & u'_{11} & 0 & u'_{12} \\ |
+ | u_{21} & 0 & u_{22} & 0 \\ |
| − | u_{21} & 0 & u_{22} & 0 \\ |
+ | 0 & u'_{21} & 0 & u'_{22} \\ |
| − | 0 & u'_{21} & 0 & u'_{22} \\ |
+ | \end{pmatrix} |
| − | \end{pmatrix} |
||
</math> |
</math> |
||
Revision as of 11:15, 20 April 2010
The geometry of interaction, GoI in short, was defined in the early nineties by Girard as an interpretation of linear logic into operators algebra: formulae were interpreted by Hilbert spaces and proofs by partial isometries.
This was a striking novelty as it was the first time that a mathematical model of logic (lambda-calculus) didn't interpret a proof of  as a morphism from A to B[1], and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on
as a morphism from A to B[1], and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on  , that is a morphism from
, that is a morphism from  to
to  . For proof composition the problem was then, given an operator on
. For proof composition the problem was then, given an operator on  and another one on
and another one on 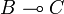 to construct a new operator on
to construct a new operator on 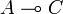 . This problem was solved by the execution formula that bares some formal analogies with Kleene's formula for recursive functions. For this reason GoI was claimed to be an operational semantics, as opposed to traditionnal denotational semantics.
. This problem was solved by the execution formula that bares some formal analogies with Kleene's formula for recursive functions. For this reason GoI was claimed to be an operational semantics, as opposed to traditionnal denotational semantics.
The first instance of the GoI was restricted to the MELL fragment of linear logic (Multiplicative and Exponential fragment) which is enough to encode lambda-calculus. Since then Girard proposed several improvements: firstly the extension to the additive connectives known as Geometry of Interaction 3 and more recently a complete reformulation using Von Neumann algebras that allows to deal with some aspects of implicit complexity
The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; in particular the execution formula appears as the composition of two automata that interact one with the other through their common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the MELL fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal.
Contents |
The Geometry of Interaction as operators
The original construction of GoI by Girard follows a general pattern already mentionned in coherent semantics under the name symmetric reducibility. First set a general space called the proof space because this is where the interpretations of proofs will live. In the case of GoI, the proof space is the space of bounded operators on 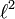 . Note that the proof space generally contains much more objects than interpretations of proofs; in the GoI case we will see that interpretations of proofs happen to be some very peculiar kind of partial isometries.
. Note that the proof space generally contains much more objects than interpretations of proofs; in the GoI case we will see that interpretations of proofs happen to be some very peculiar kind of partial isometries.
Second define a duality on this space that will be denoted as 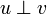 . For the GoI, two dualities have proved to work, the first one being nilpotency: two operators u and v are dual if uv is nilpotent, that is, if there is a nonegative integer n such that (uv)n = 0. We will denote by
. For the GoI, two dualities have proved to work, the first one being nilpotency: two operators u and v are dual if uv is nilpotent, that is, if there is a nonegative integer n such that (uv)n = 0. We will denote by 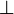 the set of nilpotent operators so that the duality reads:
the set of nilpotent operators so that the duality reads:
-
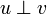 iff
iff 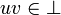 .
.
This duality applies to operators and shouldn't be confused with orthogonality of vectors. To enforce this we will reserve the notation 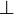 exclusively for the duality of operators and never use it for othogonality of vectors.
exclusively for the duality of operators and never use it for othogonality of vectors.
Last define a type as a subset T of the proof space that is
equal to its bidual: 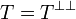 . This means that
. This means that 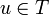 iff for all operator
iff for all operator 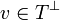 , that is such that
, that is such that
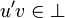 for all
for all 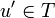 , we have
, we have 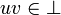 . In particular note that 0 belongs to any type.
. In particular note that 0 belongs to any type.
It remains now to interpret logical operations, that is associate a type to each formula, an object to each proof and show the adequacy lemma: if u is the interpretation of a proof of the formula A then u belongs to the type associated to A.
Preliminaries
We begin by a brief tour of the operations in Hilbert spaces that will be used in the sequel. In this article H will stand for the Hilbert space 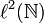 of sequences
of sequences 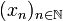 of complex numbers such that the series
of complex numbers such that the series 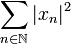 converges. If
converges. If 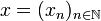 and
and 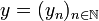 are two vectors of H we denote by
are two vectors of H we denote by 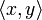 their scalar product:
their scalar product:
-
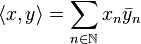 .
.
Two vectors of H are othogonal if their scalar product is nul. This notion is not to be confused with the orthogonality of operators defined above. The norm of a vector is the square root of the scalar product with itself:
-
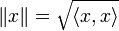 .
.
Let us denote by 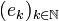 the canonical hilbertian basis of H:
the canonical hilbertian basis of H: 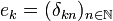 where δkn is the Kroenecker symbol. Thus if
where δkn is the Kroenecker symbol. Thus if 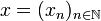 is a sequence in H we have:
is a sequence in H we have:
-
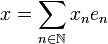 .
.
In this article we call operator on H a continuous linear map from H to H. Continuity is equivalent to the fact that operators are bounded, which means that one may define the norm of an operator u as the sup on the unit ball of the norms of its values:
-
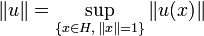 .
.
The set of (bounded) operators is denoted 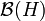 . This is our proof space.
. This is our proof space.
The range or codomain of the operator u is the set of images of vectors; the kernel of u is the set of vectors that are anihilated by u; the domain of u is the set of vectors orthogonal to the kernel:
-
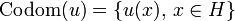 ;
;
-
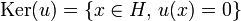 ;
;
-
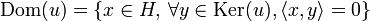 .
.
These three sets are closed subspaces of H.
The adjoint of an operator u is the operator u * defined by 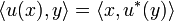 for any
for any 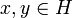 .
.
A projector is an idempotent operator of norm 0 (the projector
on the null subspace) or 1, that is an operator p
such that p2 = p and 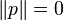 or 1. A projector is auto-adjoint and its domain is equal to its codomain.
or 1. A projector is auto-adjoint and its domain is equal to its codomain.
A partial isometry is an operator u satisfying uu * u = u; as a consequence uu * is a projector the range of which is the range of u. Similarly u * u is also a projector the range of which is the domain of u. The restriction of u to its domain is an isometry. Projectors are particular examples of partial isometries.
If u is a partial isometry then u * is also a partial isometry the domain of which is the codomain of u and the codomain of which is the domain of u.
If the domain of u is H that is if u * u = 1 we say that u has full domain, and similarly for codomain. If u and v are two partial isometries, the equation uu * + vv * = 1 means that the codomains of u and v are orthogonal and that their direct sum is H.
Partial permutations and partial isometries
It turns out that most of the operators needed to interpret logical operations are generated by partial permutations on the basis, which in particular entails that they are partial isometries.
More precisely a partial permutation 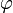 on
on 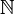 is a function defined on a subset
is a function defined on a subset 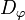 of
of 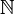 which is one-to-one onto a subset
which is one-to-one onto a subset 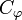 of
of 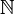 .
. 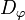 is called the domain of
is called the domain of 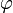 and
and 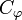 its codomain. Partial permutations may be composed: if ψ is another partial permutation on
its codomain. Partial permutations may be composed: if ψ is another partial permutation on 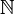 then
then  is defined by:
is defined by:
-
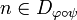 iff
iff 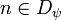 and
and 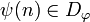 ;
;
- if
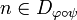 then
then 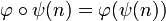 ;
;
- the codomain of
 is the image of the domain.
is the image of the domain.
Partial permutations are well known to form a structure of inverse monoid that we detail now.
A partial identitie is a partial permutation 1D whose domain and codomain are both equal to a subset D on which 1D is the identity function. Partial identities are idempotent for composition.
Among partial identities one finds the identity on the empty subset, that is the empty map, that we will denote as 0 and the identity on 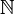 that we will denote by 1. This latter permutation is the neutral for composition.
that we will denote by 1. This latter permutation is the neutral for composition.
If 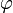 is a partial permutation there is an inverse partial permutation
is a partial permutation there is an inverse partial permutation 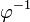 whose domain is
whose domain is 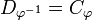 and who satisfies:
and who satisfies:
Given a partial permutation 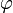 one defines a partial isometry
one defines a partial isometry 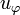 by:
by:
In other terms if 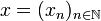 is a sequence in
is a sequence in 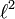 then
then 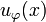 is the sequence
is the sequence 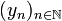 defined by:
defined by:
-
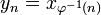 if
if 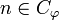 , 0 otherwise.
, 0 otherwise.
We will (not so abusively) write 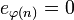 when
when 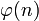 is undefined.
is undefined.
The domain of 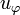 is the subspace spaned by the family
is the subspace spaned by the family 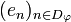 and the codomain of
and the codomain of 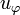 is the subspace spaned by
is the subspace spaned by 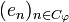 . As a particular case if
. As a particular case if 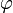 is 1D the partial identity on D then
is 1D the partial identity on D then 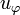 is the projector on the subspace spaned by
is the projector on the subspace spaned by 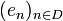 .
.
If ψ is another partial permutation then we have:
-
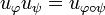 .
.
If  is a partial permutation then the adjoint of
is a partial permutation then the adjoint of 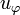 is:
is:
-
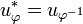 .
.
In particular the projector on the domain of 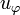 is given by:
is given by:
-
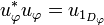 .
.
and similarly the projector on the codomain of 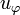 is:
is:
-
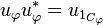 .
.
Proposition
Let 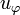 and uψ be two partial isometries generated by partial permutations. Then we have:
and uψ be two partial isometries generated by partial permutations. Then we have:
-
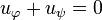 iff
iff 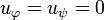 ,
,
that is iff 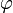 and ψ are the nowhere defined partial permutation.
and ψ are the nowhere defined partial permutation.
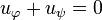 then for any n we have
then for any n we have 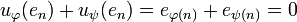 which is possible only if
which is possible only if 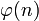 and ψ(n) are undefined.
and ψ(n) are undefined.
From operators to matrices: internalization/externalization
It will be convenient to view operators on H as acting on 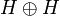 , and conversely. For this purpose we define an isomorphism
, and conversely. For this purpose we define an isomorphism 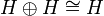 by
by 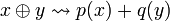 where
where 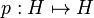 and
and 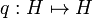 are partial isometries given by:
are partial isometries given by:
- p(en) = e2n,
- q(en) = e2n + 1.
From the definition p and q have full domain, that is satisfy p * p = q * q = 1. On the other hand their codomains are orthogonal, thus we have p * q = q * p = 0. Note that we also have pp * + qq * = 1.
The choice of p and q is actually arbitrary, any two partial isometries with full domain and orthogonal codomains would do the job.
Let U be an operator on 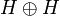 . We can write U as a matrix:
. We can write U as a matrix:
where each uij operates on H.
Now through the isomorphism 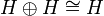 we may transform U into the operator u on H defined by:
we may transform U into the operator u on H defined by:
- u = pu11p * + pu12q * + qu21p * + qu22q * .
We call u the internalization of U. Internalization is compatible with composition (functorial so to speak): if V is another operator on 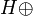 then the internalization of the matrix product UV is the product uv.
then the internalization of the matrix product UV is the product uv.
Conversely given an operator u on H we may externalize it obtaining an operator U on 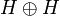 :
:
- u11 = p * up;
- u12 = p * uq;
- u21 = q * up;
- u22 = q * uq.
Interpreting the multiplicative connectives
Recall that when u and v are operators we denote by 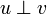 the fact that uv is nilpotent, and that
the fact that uv is nilpotent, and that 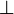 denotes the set of nilpotent operators so that
denotes the set of nilpotent operators so that 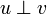 iff
iff 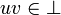 .
.
If X is set of operators also recall that 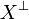 denotes the set of dual operators:
denotes the set of dual operators:
-
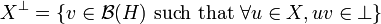 .
.
There are a few properties of this duality that we will use without mention in the sequel; let X and Y be sets of operators:
-
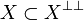 ;
;
-
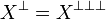 .
.
- if
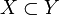 then
then 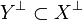 ;
;
In particular 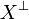 is always a type (equal to its biorthogonal). We say that X generates the type
is always a type (equal to its biorthogonal). We say that X generates the type 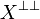 .
.
The tensor and the linear application
Given two types A and B two types, we define their tensor by:
Note the closure by biorthogonal to make sure that we obtain a type. From what precedes we see that 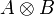 is generated by the internalizations of operators on
is generated by the internalizations of operators on 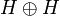 of the form:
of the form:
This is an abuse of notations as this operation is more like a direct sum than a tensor. We will stick to this notation though because it defines the interpretation of the tensor connective of linear logic.
The linear implication is derived from the tensor by duality: given two types A and B the type  is defined by:
is defined by:
-
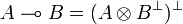 .
.
Unfolding this definition we see that we have:
-
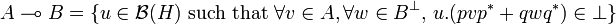 .
.
The idendity
The interpretation of the identity is an example of the internalization/externalization procedure. Given a type A we are to find an operator ι in type 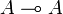 , thus satisfying:
, thus satisfying:
-
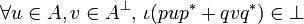 .
.
An easy solution is to take ι = pq * + qp * . In this way we get ι(pup * + qvq * ) = qup * + pvq * . Therefore (ι(pup * + qvq * ))2 = quvq * + pvup * , from which one deduces that this operator is nilpotent iff uv is nilpotent. It is the case since u is in A and v in 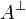 .
.
It is interesting to note that the ι thus defined is actually the internalization of the operator on 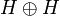 given by the matrix:
given by the matrix:
-
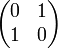 .
.
We will see once the composition is defined that the ι operator is the interpretation of the identity proof, as expected.
The execution formula, version 1: application
Let A and B be two types and u an operator in  . By definition this means that given v in A and w in
. By definition this means that given v in A and w in 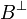 the operator u.(pvp * + qwq * ) is nilpotent.
the operator u.(pvp * + qwq * ) is nilpotent.
Let us define u11 to u22 by externalization as above. If we compute (u.(pvp * + qwq * ))n we see that this is a finite sum of operators of the form:
-
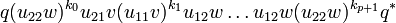 ,
,
-
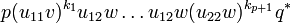 ,
,
-
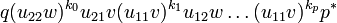 or
or
-
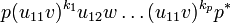
where each of these monimials has exactly n factors of the form ui1v or ui2w.
From the nilpotency of u.(pvp * + qwq * ) we deduce that u11v is nilpotent by considering the particular case where w = 0. We also have that q * (u.(pvp * + qwq * ))nq is null for n big enough, which means that monomials of type 1 above are null as soon as their length (the number of factors of the form ui1v or ui2w) is bigger than n.
This implies that the two following operators are nilpotent:
- u11v and
-
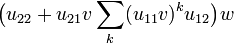 .
.
Conversely if these two operators are nilpotent then one can show that so is u.(pvp * + qwq * ). Moreover we have:
-
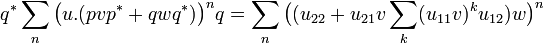 .
.
We define the application of u to v as:
-
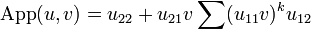 .
.
Note that this is well defined as soon as u11v is nilpotent.
We summarize what has just been shown in the following theorem:
Theorem
Let u be an operator, A and B be two types; the following conditions are equivalent:
-
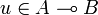 ;
;
- for any
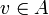 , we both have:
, we both have:
- u11v is nilpotent and
-
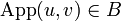 .
.
Corollary
Under the hypothesis of the theorem we have:
-
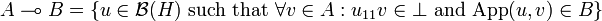 .
.
As an example if we compute the application of the interpretation of the identity ι in type 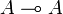 to the operator
to the operator 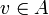 then we have:
then we have:
-
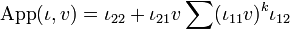 .
.
Now recall that ι = pq * + qp * so that ι11 = ι22 = 0 and ι12 = ι21 = 1 and we thus get:
- App(ι,v) = v
as expected.
The tensor rule
Let now A,A',B and B' be types and consider two operators u and u' respectively in  and
and 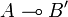 . We define an operator denoted
. We define an operator denoted 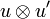 by:
by:
Once again the notation is motivated by linear logic syntax and is contradictory with linear algebra practice since what we denote by 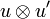 actually is the internalization of the direct sum
actually is the internalization of the direct sum 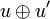 .
.
Indeed if we think of u and u' as the internalizations of the matrices:
-
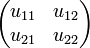 and
and 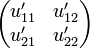
then we may write:
Thus the components of 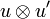 are given by:
are given by:
-
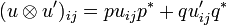 .
.
and we see that 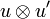 is actually the internalization of the matrix:
is actually the internalization of the matrix:
We are now to show that if we suppose uand u' are in types  and
and 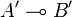 , then
, then 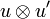 is in
is in 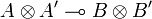 . For this we consider v and v' in respectively in A and A', so that pvp * + qv'q * is in
. For this we consider v and v' in respectively in A and A', so that pvp * + qv'q * is in 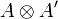 , and we show that
, and we show that 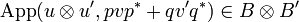 .
.
Since u and u' are in  and
and 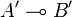 we have that App(u,v) and App(u',v') are respectively in B and B', thus:
we have that App(u,v) and App(u',v') are respectively in B and B', thus:
-
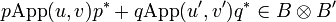 .
.
We know that both u11v and u'11v' are nilpotent. But we have:
Therefore 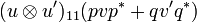 is nilpotent. So we can compute
is nilpotent. So we can compute 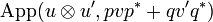 :
:
thus lives in 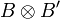 .
.
Other monoidal constructions
Let σ be the operator:
- σ = ppq * q * + pqp * q * + qpq * p * + qqp * p * .
One can check that σ is the internalization of the operator S on 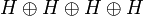 defined by:
defined by: 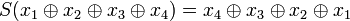 . In particular the components of σ are:
. In particular the components of σ are:
- σ11 = σ22 = 0;
- σ12 = σ21 = pq * + qp * .
Let A and B be types and u and v be operators in A and B. Then pup * + qvq * is in 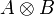 and as σ11.(pup * + qvq * ) = 0 we may compute:
and as σ11.(pup * + qvq * ) = 0 we may compute:
But 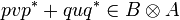 , thus we have shown that:
, thus we have shown that:
-
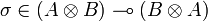 .
.
We can get distributivity by considering the operator:
- δ = ppp * p * q * + pqpq * p * q * + pqqq * q * + qppp * p * + qpqp * q * p * + qqq * q * p *
that is similarly shown to be in type 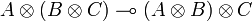 for any types A, B and C.
for any types A, B and C.
We can finally get weak distributivity thanks to the operators:
- δ1 = pppp * q * + ppqp * q * q * + pqq * q * q * + qpp * p * p * + qqpq * p * p * + qqqq * p * and
- δ2 = ppp * p * q * + pqpq * p * q * + pqqq * q * + qppp * p * + qpqp * q * p * + qqq * q * p * .
Given three types A, B and C then one can show that:
- δ1 has type
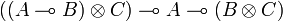 and
and
- δ2 has type
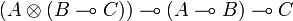 .
.
The Geometry of Interaction as an abstract machine
Cite error:
<ref> tags exist, but no <references/> tag was found