Isomorphism
From LLWiki
(Difference between revisions)
Lionel Vaux (Talk | contribs) (stub) |
Lionel Vaux (Talk | contribs) m (added template stub) |
||
| Line 1: | Line 1: | ||
| + | {{stub}} |
||
| + | |||
Two formulas <math>A</math> and <math>B</math> are isomorphic, when there are two proofs <math>\pi</math> of <math>A \vdash B</math> and <math>\rho</math> of <math>B \vdash A</math> such that eliminating the cut on <math>A</math> in |
Two formulas <math>A</math> and <math>B</math> are isomorphic, when there are two proofs <math>\pi</math> of <math>A \vdash B</math> and <math>\rho</math> of <math>B \vdash A</math> such that eliminating the cut on <math>A</math> in |
||
Revision as of 14:38, 16 October 2009
This page is a stub and needs more content.
Two formulas A and B are isomorphic, when there are two proofs π of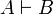 
and ρ of 
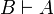such that eliminating the cut on A in
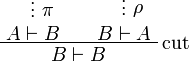
leads to an η-expansion of
,
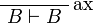and eliminating the cut on B in
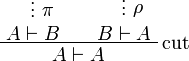
leads to an η-expansion of
.
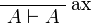Some well known isomorphisms of linear logic are the following ones:
-
- …
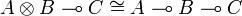
