Isomorphism
From LLWiki
(Difference between revisions)
Lionel Vaux (Talk | contribs) m (added template stub) |
(Link to list of isomorphisms) |
||
| (One intermediate revision by one user not shown) | |||
| Line 1: | Line 1: | ||
{{stub}} |
{{stub}} |
||
| − | Two formulas <math>A</math> and <math>B</math> are isomorphic, when there are two proofs <math>\pi</math> of <math>A \vdash B</math> and <math>\rho</math> of <math>B \vdash A</math> such that eliminating the cut on <math>A</math> in |
+ | Two formulas <math>A</math> and <math>B</math> are isomorphic (denoted <math>A\cong B</math>), when there are two proofs <math>\pi</math> of <math>A \vdash B</math> and <math>\rho</math> of <math>B \vdash A</math> such that eliminating the cut on <math>A</math> in |
<math>\AxRule{}\VdotsRule{\pi}{A \vdash B}\AxRule{}\VdotsRule{\rho}{B \vdash A}\LabelRule{\rulename{cut}}\BinRule{B\vdash B}\DisplayProof</math> |
<math>\AxRule{}\VdotsRule{\pi}{A \vdash B}\AxRule{}\VdotsRule{\rho}{B \vdash A}\LabelRule{\rulename{cut}}\BinRule{B\vdash B}\DisplayProof</math> |
||
| Line 17: | Line 17: | ||
<math>\LabelRule{\rulename{ax}}\NulRule{A\vdash A}\DisplayProof</math>. |
<math>\LabelRule{\rulename{ax}}\NulRule{A\vdash A}\DisplayProof</math>. |
||
| − | Some well known isomorphisms of linear logic are the following ones: |
+ | Linear logic admits [[List of isomorphisms|many isomorphisms]], but it is not known wether all of them have been discovered or not. |
| − | * <math>A\tens B \limp C \cong A\limp B \limp C</math> |
||
| − | * … |
||
Latest revision as of 20:38, 25 April 2013
This page is a stub and needs more content.
Two formulas A and B are isomorphic (denoted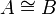 
), when there are two proofs π of 
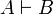and ρ of 
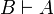such that eliminating the cut on A in
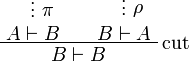
leads to an η-expansion of
,
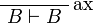and eliminating the cut on B in
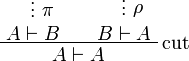
leads to an η-expansion of
.
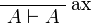Linear logic admits many isomorphisms, but it is not known wether all of them have been discovered or not.
