Regular formula
From LLWiki
A regular formula is a formula R such that 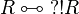 .
.
A formula L is co-regular if its dual 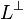 is regular, that is if
is regular, that is if 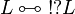 .
.
Alternative characterization
R is regular if and only if it is equivalent to a formula of the shape 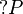 for some positive formula P.
for some positive formula P.
Proof.
If R is regular then 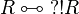 with
with 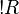 positive. If
positive. If 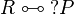 with P positive then R is regular since
with P positive then R is regular since 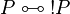 .
.
Regular connectives
A connective c of arity n is regular if for any regular formulas R1,...,Rn, 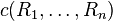 is regular.
is regular.
Proposition (Regular connectives)
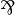 ,
, 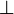 and
and 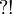 define regular connectives.
define regular connectives.
Proof.
If R and S are regular, 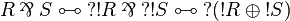 thus it is regular since
thus it is regular since 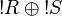 is positive.
is positive.
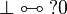 thus it is regular since
thus it is regular since 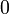 is positive.
is positive.
If R is regular then 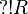 is regular, since
is regular, since 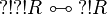 .
.
More generally, 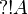 is regular for any formula A.
is regular for any formula A.