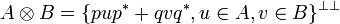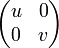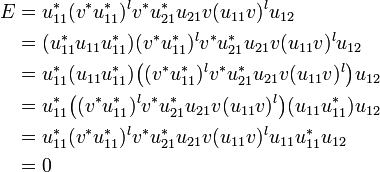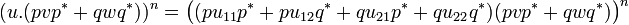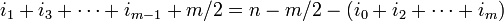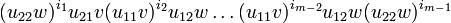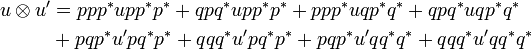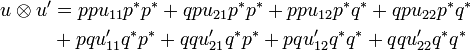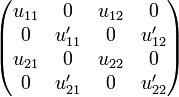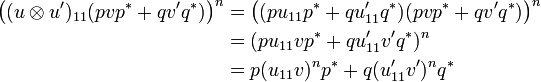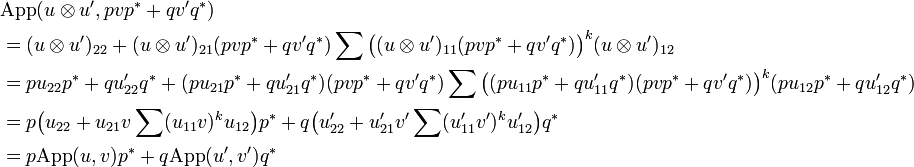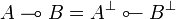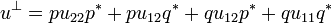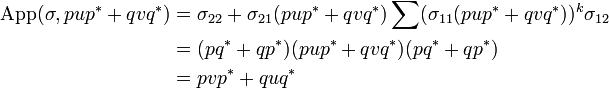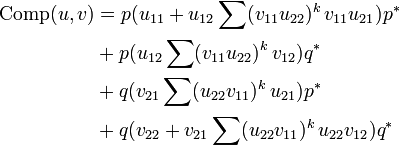GoI for MELL: the *-autonomous structure
Recall that when u and v are p-isometries we say they are dual when uv is nilpotent, and that 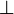 denotes the set of nilpotent operators. A type is a subset of
denotes the set of nilpotent operators. A type is a subset of 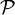 that is equal to its bidual. In particular
that is equal to its bidual. In particular 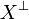 is a type for any
is a type for any 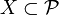 . We say that X generates the type
. We say that X generates the type 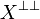 .
.
Contents |
The tensor and the linear application
If u and v are two p-isometries summing them doesn't in general produces a p-isometry. However as pup * and qvq * have disjoint domains and disjoint codomains it is true that pup * + qvq * is a p-isometry. Given two types A and B, we thus define their tensor by:
Note the closure by bidual to make sure that we obtain a type.
From what precedes we see that 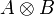 is generated by the internalizations of operators on
is generated by the internalizations of operators on 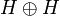 of the form:
of the form:
Remark: This so-called tensor resembles a sum rather than a product. We will stick to this terminology though because it defines the interpretation of the tensor connective of linear logic.
The linear implication is derived from the tensor by duality: given two types A and B the type  is defined by:
is defined by:
-
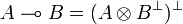 .
.
Unfolding this definition we get:
-
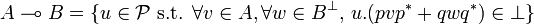 .
.
The identity
Given a type A we are to find an operator ι in type 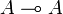 , thus satisfying:
, thus satisfying:
-
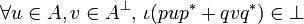 .
.
An easy solution is to take ι = pq * + qp * . In this way we get ι(pup * + qvq * ) = qup * + pvq * . Therefore (ι(pup * + qvq * ))2 = quvq * + pvup * , from which one deduces that this operator is nilpotent iff uv is nilpotent. It is the case since u is in A and v in 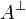 .
.
It is interesting to note that the ι thus defined is actually the internalization of the operator on 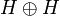 given by the matrix:
given by the matrix:
-
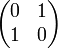 .
.
We will see once the composition is defined that the ι operator is the interpretation of the identity proof, as expected.
The execution formula, version 1: application
Definition
Let u and v be two operators; as above denote by uij the external components of u. If u11v is nilpotent we define the application of u to v by:
| App(u,v) = u22 + u21v | ∑ | (u11v)ku12 |
| k |
.
Note that the hypothesis that u11v is nilpotent entails that the sum
| ∑ | (u11v)k |
| k |
is actually finite. It would be enough to assume that this sum converges. For simplicity we stick to the nilpotency condition, but we should mention that weak nilpotency would do as well.
Theorem
If u and v are p-isometries such that u11v is nilpotent, then App(u,v) is also a p-isometry.
Proof. Let us note Ek = u21v(u11v)ku12. Recall that u22 and u12 being external components of the p-isometry u, they have disjoint domains. Thus it is also the case of u22 and Ek. Similarly u22 and Ek have disjoint codomains because u22 and u21 have disjoint codomains.
Let now k and l be two integers such that k > l and let us compute for example the intersection of the codomains of Ek and El:
As k > l we may write 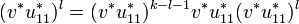 . Let us note
. Let us note 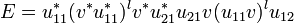 so that
so that 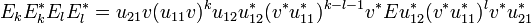 . We have:
. We have:
because u11 and u12 have disjoint codomains, thus 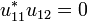 .
.
Similarly we can show that Ek and El have disjoint domains. Therefore we have proved that all terms of the sum App(u,v) have disjoint domains and disjoint codomains. Consequently App(u,v) is a p-isometry.
Theorem
Let A and B be two types and u a p-isometry. Then the two following conditions are equivalent:
-
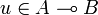 ;
;
- for any
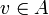 we have:
we have:
- u11v is nilpotent and
-
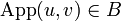 .
.
Proof. Let v and w be two p-isometries. If we compute
we get a finite sum of monomial operators of the form:
-
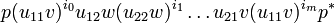
-
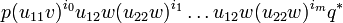 ,
,
-
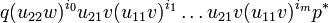 or
or
-
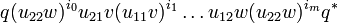 ,
,
for all tuples of (nonnegative) integers 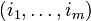 such that
such that 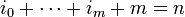 .
.
Each of these monomial is a p-isometry. Furthermore they have disjoint domains and disjoint codomains because their sum is the p-isometry (u.(pvp * + qwq * ))n. This entails that (u.(pvp * + qwq * ))n = 0 iff all these monomials are null.
Suppose u11v is nilpotent and consider:
-
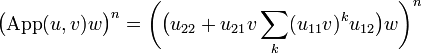 .
.
Developping we get a finite sum of monomials of the form:
- 5.
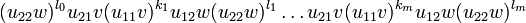
for all tuples 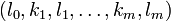 such that
such that 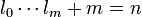 and ki is less than the degree of nilpotency of u11v for all i.
and ki is less than the degree of nilpotency of u11v for all i.
Again as these monomials are p-isometries and their sum is the p-isometry (App(u,v)w)n, they have pairwise disjoint domains and pairwise disjoint codomains. Note that each of these monomial is equal to q * Mq where M is a monomial of type 4 above.
As before we thus have that 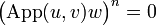 iff all monomials of type 5 are null.
iff all monomials of type 5 are null.
Suppose now that 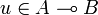 and
and 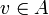 . Then, since
. Then, since 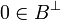 (0 belongs to any type) u.(pvp * ) = pu11vp * is nilpotent, thus u11v is nilpotent.
(0 belongs to any type) u.(pvp * ) = pu11vp * is nilpotent, thus u11v is nilpotent.
Suppose further that 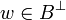 . Then u.(pvp * + qwq * ) is nilpotent, thus there is a N such that (u.(pvp * + qwq * ))n = 0 for any
. Then u.(pvp * + qwq * ) is nilpotent, thus there is a N such that (u.(pvp * + qwq * ))n = 0 for any 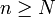 . This entails that all monomials of type 1 to 4 are null. Therefore all monomials appearing in the developpment of (App(u,v)w)N are null which proves that App(u,v)w is nilpotent. Thus
. This entails that all monomials of type 1 to 4 are null. Therefore all monomials appearing in the developpment of (App(u,v)w)N are null which proves that App(u,v)w is nilpotent. Thus 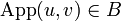 .
.
Conversely suppose for any 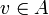 and
and 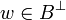 , u11v and App(u,v)w are nilpotent. Let P and N be their respective degrees of nilpotency and put n = N(P + 1) + N. Then we claim that all monomials of type 1 to 4 appearing in the development of (u.(pvp * + qwq * ))n are null.
, u11v and App(u,v)w are nilpotent. Let P and N be their respective degrees of nilpotency and put n = N(P + 1) + N. Then we claim that all monomials of type 1 to 4 appearing in the development of (u.(pvp * + qwq * ))n are null.
Consider for example a monomial of type 1:
with 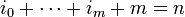 . Note that m must be even.
. Note that m must be even.
If 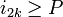 for some
for some 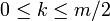 then
then 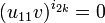 thus our monomial is null. Otherwise if i2k < P for all k we have:
thus our monomial is null. Otherwise if i2k < P for all k we have:
thus:
-
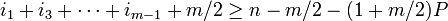 .
.
Now if 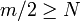 then
then 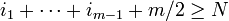 . Otherwise
. Otherwise 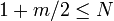 thus
thus
-
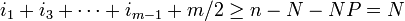 .
.
Since N is the degree of nilpotency of App(u,v)w we have that the monomial:
is null, thus also the monomial of type 1 we started with.
Corollary
If A and B are types then we have:
-
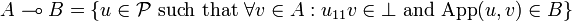 .
.
As an example if we compute the application of the interpretation of the identity ι in type 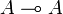 to the operator
to the operator 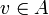 then we have:
then we have:
-
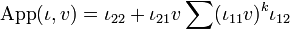 .
.
Now recall that ι = pq * + qp * so that ι11 = ι22 = 0 and ι12 = ι21 = 1 and we thus get:
- App(ι,v) = v
as expected.
The tensor rule
Let now A,A',B and B' be types and consider two operators u and u' respectively in  and
and 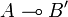 . We define an operator
. We define an operator 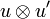 by:
by:
Once again the notation is motivated by linear logic syntax and is contradictory with linear algebra practice since what we denote by 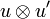 actually is the internalization of the direct sum
actually is the internalization of the direct sum 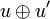 .
.
Indeed if we think of u and u' as the internalizations of the matrices:
-
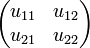 and
and 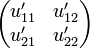
then we may write:
Thus the components of 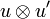 are given by:
are given by:
-
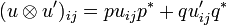 .
.
and we see that 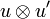 is actually the internalization of the matrix:
is actually the internalization of the matrix:
We are now to show that if we suppose uand u' are in types  and
and 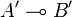 , then
, then 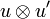 is in
is in 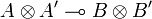 . For this we consider v and v' respectively in A and A', so that pvp * + qv'q * is in
. For this we consider v and v' respectively in A and A', so that pvp * + qv'q * is in 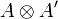 , and we show that
, and we show that 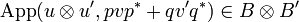 .
.
Since u and u' are in  and
and 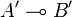 we have that u11v and u'11v' are nilpotent and that App(u,v) and App(u',v') are respectively in B and B', thus:
we have that u11v and u'11v' are nilpotent and that App(u,v) and App(u',v') are respectively in B and B', thus:
-
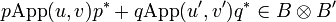 .
.
But we have:
Therefore 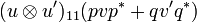 is nilpotent. So we can compute
is nilpotent. So we can compute 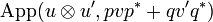 :
:
thus lives in 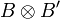 .
.
Other monoidal constructions
Contraposition
Let A and B be some types; we have:
Indeed, 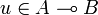 means that for any v and w in respectively A and
means that for any v and w in respectively A and 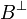 we have
we have 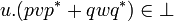 which is exactly the definition of
which is exactly the definition of 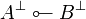 .
.
We will denote 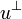 the operator:
the operator:
where uij is given by externalization. Therefore the externalization of 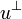 is:
is:
-
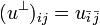 where
where  is defined by
is defined by 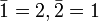 .
.
From this we deduce that 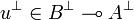 and that
and that 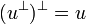 .
.
Commutativity
Let σ be the operator:
- σ = ppq * q * + pqp * q * + qpq * p * + qqp * p * .
One can check that σ is the internalization of the operator S on 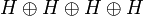 defined by:
defined by: 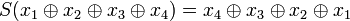 . In particular the components of σ are:
. In particular the components of σ are:
- σ11 = σ22 = 0;
- σ12 = σ21 = pq * + qp * .
Let A and B be types and u and v be operators in A and B. Then pup * + qvq * is in 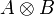 and as σ11.(pup * + qvq * ) = 0 we may compute:
and as σ11.(pup * + qvq * ) = 0 we may compute:
But 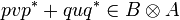 , thus we have shown that:
, thus we have shown that:
-
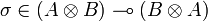 .
.
Distributivity
We get distributivity by considering the operator:
- δ = ppp * p * q * + pqpq * p * q * + pqqq * q * + qppp * p * + qpqp * q * p * + qqq * q * p *
that is similarly shown to be in type 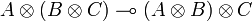 for any types A, B and C.
for any types A, B and C.
Weak distributivity
Similarly we get weak distributivity thanks to the operators:
- δ1 = pppp * q * + ppqp * q * q * + pqq * q * q * + qpp * p * p * + qqpq * p * p * + qqqq * p * and
- δ2 = ppp * p * q * + pqpq * p * q * + pqqq * q * + qppp * p * + qpqp * q * p * + qqq * q * p * .
Given three types A, B and C then one can show that:
- δ1 has type
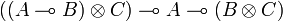 and
and
- δ2 has type
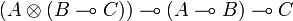 .
.
Execution formula, version 2: composition
Let A, B and C be types and u and v be operators respectively in types  and
and 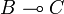 .
.
As usual we will denote uij and vij the operators obtained by externalization of u and v, eg, u11 = p * up, ...
As u is in  we have that
we have that 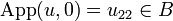 ; similarly as
; similarly as 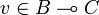 , thus
, thus 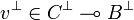 , we have
, we have 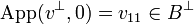 . Thus u22v11 is nilpotent.
. Thus u22v11 is nilpotent.
We define the operator Comp(u,v) by:
This is well defined since u11v22 is nilpotent. As an example let us compute the composition of u and ι in type 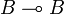 ; recall that ιij = δij, so we get:
; recall that ιij = δij, so we get:
- Comp(u,ι) = pu11p * + pu12q * + qu21p * + qu22q * = u
Similar computation would show that Comp(ι,v) = v (we use pp * + qq * = 1 here).
Coming back to the general case we claim that Comp(u,v) is in 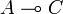 : let a be an operator in A. By computation we can check that:
: let a be an operator in A. By computation we can check that:
- App(Comp(u,v),a) = App(v,App(u,a)).
Now since u is in  , App(u,a) is in B and since v is in
, App(u,a) is in B and since v is in 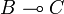 , App(v,App(u,a)) is in C.
, App(v,App(u,a)) is in C.
If we now consider a type D and an operator w in 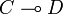 then we have:
then we have:
- Comp(Comp(u,v),w) = Comp(u,Comp(v,w)).
Putting together the results of this section we finally have:
Theorem
Let GoI(H) be defined by:
- objects are types, ie sets A of p-isometries satisfying:
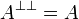 ;
;
- morphisms from A to B are p-isometries in type
 ;
;
- composition is given by the formula above.
Then GoI(H) is a star-autonomous category.