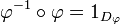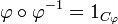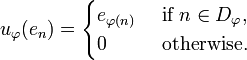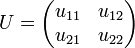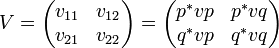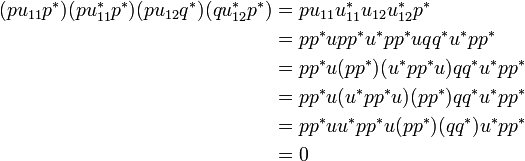GoI for MELL: partial isometries
Contents |
Operators, partial isometries
We will denote by H the Hilbert space 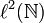 of sequences
of sequences 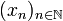 of complex numbers such that the series
of complex numbers such that the series 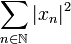 converges. If
converges. If 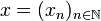 and
and 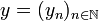 are two vectors of H their scalar product is:
are two vectors of H their scalar product is:
-
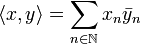 .
.
Two vectors of H are othogonal if their scalar product is nul. We will say that two subspaces are disjoint when any two vectors taken in each subspace are orthorgonal. Note that this notion is different from the set theoretic one, in particular two disjoint subspaces always have exactly one vector in common: 0.
The norm of a vector is the square root of the scalar product with itself:
-
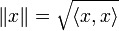 .
.
Let us denote by 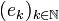 the canonical hilbertian basis of H:
the canonical hilbertian basis of H: 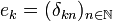 where δkn is the Kroenecker symbol: δkn = 1 if k = n, 0 otherwise. Thus if
where δkn is the Kroenecker symbol: δkn = 1 if k = n, 0 otherwise. Thus if 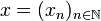 is a sequence in H we have:
is a sequence in H we have:
-
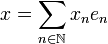 .
.
An operator on H is a continuous linear map from H to H.[1]The set of (bounded) operators is denoted by 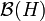 .
.
The range or codomain of the operator u is the set of images of vectors; the kernel of u is the set of vectors that are anihilated by u; the domain of u is the set of vectors orthogonal to the kernel, ie, the maximal subspace disjoint with the kernel:
-
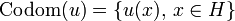 ;
;
-
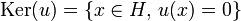 ;
;
-
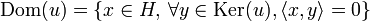 .
.
These three sets are closed subspaces of H.
The adjoint of an operator u is the operator u * defined by 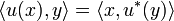 for any
for any 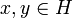 . Adjointness is well behaved w.r.t. composition of operators:
. Adjointness is well behaved w.r.t. composition of operators:
- (uv) * = v * u * .
A projector is an idempotent operator of norm 0 (the projector
on the null subspace) or 1, that is an operator p
such that p2 = p and 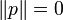 or 1. A projector is auto-adjoint and its domain is equal to its codomain.
or 1. A projector is auto-adjoint and its domain is equal to its codomain.
A partial isometry is an operator u satisfying uu * u = u; this condition entails that we also have u * uu * = u * . As a consequence uu * and uu * are both projectors, called respectively the initial and the final projector of u because their (co)domains are respectively the domain and the codomain of u:
- Dom(u * u) = Codom(u * u) = Dom(u);
- Dom(uu * ) = Codom(uu * ) = Codom(u).
The restriction of u to its domain is an isometry. Projectors are particular examples of partial isometries.
If u is a partial isometry then u * is also a partial isometry the domain of which is the codomain of u and the codomain of which is the domain of u.
If the domain of u is H that is if u * u = 1 we say that u has full domain, and similarly for codomain. If u and v are two partial isometries then we have:
- uv * = 0 iff u * uv * v = 0 iff the domains of u and v are disjoint;
- u * v = 0 iff uu * vv * = 0 iff the codomains of u and v are disjoint;
- uu * + vv * = 1 iff the codomains of u and v are disjoint and their their direct sum is H.
Partial permutations
We will now define our proof space which turns out to be the set of partial isometries acting as permutations on the canonical basis 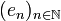 .
.
More precisely a partial permutation 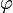 on
on 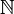 is a one-to-one map defined on a subset
is a one-to-one map defined on a subset 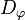 of
of 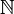 onto a subset
onto a subset 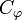 of
of 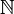 .
. 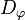 is called the domain of
is called the domain of 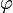 and
and 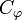 its codomain. Partial permutations may be composed: if ψ is another partial permutation on
its codomain. Partial permutations may be composed: if ψ is another partial permutation on 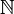 then
then  is defined by:
is defined by:
-
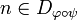 iff
iff 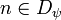 and
and 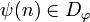 ;
;
- if
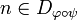 then
then 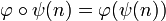 ;
;
- the codomain of
 is the image of the domain:
is the image of the domain: 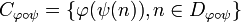 .
.
Partial permutations are well known to form a structure of inverse monoid that we detail now.
Given a a subset D of 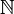 , the partial identity on D is the partial permutation
, the partial identity on D is the partial permutation 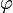 defined by:
defined by:
-
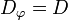 ;
;
-
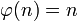 for any
for any 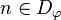 .
.
Thus the codomain of 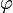 is D.
is D.
The partial identity on D will be denoted by 1D. Partial identities are idempotent for composition.
Among partial identities one finds the identity on the empty subset, that is the empty map, that we will denote by 0 and the identity on 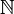 that we will denote by 1. This latter permutation is the neutral for composition.
that we will denote by 1. This latter permutation is the neutral for composition.
If 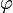 is a partial permutation there is an inverse partial permutation
is a partial permutation there is an inverse partial permutation 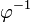 whose domain is
whose domain is 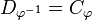 and who satisfies:
and who satisfies:
The proof space
Given a partial permutation 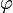 one defines a partial isometry
one defines a partial isometry 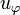 by:
by:
In other terms if 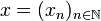 is a sequence in
is a sequence in 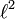 then
then 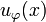 is the sequence
is the sequence 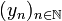 defined by:
defined by:
-
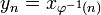 if
if 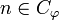 , 0 otherwise.
, 0 otherwise.
We will (not so abusively) write 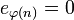 when
when 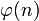 is undefined so that the definition of
is undefined so that the definition of 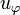 reads:
reads:
-
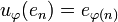 .
.
The domain of 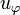 is the subspace spanned by the family
is the subspace spanned by the family 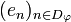 and the codomain of
and the codomain of 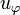 is the subspace spanned by
is the subspace spanned by 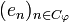 . In particular if
. In particular if 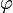 is 1D then
is 1D then 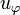 is the projector on the subspace spanned by
is the projector on the subspace spanned by 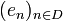 .
.
Definition
We call p-isometry a partial isometry of the form 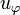 where
where 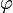 is a partial permutation on
is a partial permutation on 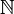 . The proof space
. The proof space 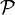 is the set of all p-isometries.
is the set of all p-isometries.
Proposition
Let 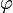 and ψ be two partial permutations. We have:
and ψ be two partial permutations. We have:
-
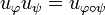 .
.
The adjoint of 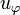 is:
is:
-
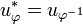 .
.
In particular the initial projector of 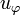 is given by:
is given by:
-
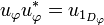 .
.
and the final projector of 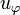 is:
is:
-
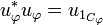 .
.
If p is a projector in 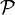 then there is a partial identity 1D such that
then there is a partial identity 1D such that 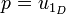 .
.
Projectors commute, in particular we have:
-
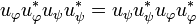 .
.
Note that this entails all the other commutations of projectors: 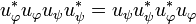 and
and 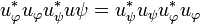 .
.
In particular note that 0 is a p-isometry. The set 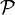 is a submonoid of
is a submonoid of 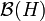 but it is not a subalgebra.[2]In general given
but it is not a subalgebra.[2]In general given 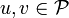 we don't necessarily have
we don't necessarily have 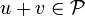 . However we have:
. However we have:
Proposition
Let 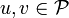 . Then
. Then 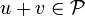 iff u and v have disjoint domains and disjoint codomains, that is:
iff u and v have disjoint domains and disjoint codomains, that is:
-
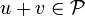 iff uu * vv * = u * uv * v = 0.
iff uu * vv * = u * uv * v = 0.
Proof. Suppose for contradiction that en is in the domains of u and v. There are integers p and q such that u(en) = ep and v(en) = eq thus (u + v)(en) = ep + eq which is not a basis vector; therefore u + v is not a p-permutation.
As a corollary note that if u + v = 0 then u = v = 0.
From operators to matrices: internalization/externalization
It will be convenient to view operators on H as acting on 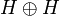 , and conversely. For this purpose we define an isomorphism
, and conversely. For this purpose we define an isomorphism 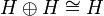 by
by 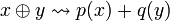 where
where 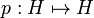 and
and 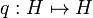 are partial isometries given by:
are partial isometries given by:
- p(en) = e2n,
- q(en) = e2n + 1.
From the definition p and q have full domain, that is satisfy p * p = q * q = 1. On the other hand their codomains are disjoint, thus we have p * q = q * p = 0. As the sum of their codomains is the full space H we also have pp * + qq * = 1.
Note that we have choosen p and q in 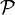 . However the choice is arbitrary: any two p-isometries with full domain and disjoint codomains would do the job.
. However the choice is arbitrary: any two p-isometries with full domain and disjoint codomains would do the job.
Given an operator u on H we may externalize it obtaining an operator U on 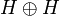 defined by the matrix:
defined by the matrix:
where the uij's are given by:
- u11 = p * up;
- u12 = p * uq;
- u21 = q * up;
- u22 = q * uq.
The uij's are called the external components of u. The externalization is functorial in the sense that if v is another operator externalized as:
then the externalization of uv is the matrix product UV.
As pp * + qq * = 1 we have:
- u = (pp * + qq * )u(pp * + qq * ) = pu11p * + pu12q * + qu21p * + qu22q *
which entails that externalization is reversible, its converse being called internalization.
If we suppose that u is a p-isometry then so are the components uij's. Thus the formula above entails that the four terms of the sum have pairwise disjoint domains and pairwise disjoint codomains from which we deduce:
Proposition
If u is a p-isometry and uij are its external components then:
- u1j and u2j have disjoint domains, that is
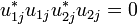 for j = 1,2;
for j = 1,2;
- ui1 and ui2 have disjoint codomains, that is
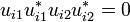 for i = 1,2.
for i = 1,2.
As an example of computation in 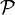 let us check that the product of the final projectors of pu11p * and pu12q * is null:
let us check that the product of the final projectors of pu11p * and pu12q * is null:
where we used the fact that all projectors in 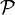 commute, which is in particular the case of pp * and u * pp * u.
commute, which is in particular the case of pp * and u * pp * u.
Notes and references
- ↑ Continuity is equivalent to the fact that operators are bounded, which means that one may define the norm of an operator u as the sup on the unit ball of the norms of its values:
-
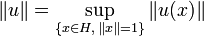 .
.
-
- ↑
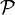 is the normalizing groupoid of the maximal commutative subalgebra of
is the normalizing groupoid of the maximal commutative subalgebra of 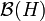 consisiting of all operators diagonalizable in the canonical basis.
consisiting of all operators diagonalizable in the canonical basis.