Lattice of exponential modalities
(Proof sketches) |
m (Pointer to list of equivalences) |
||
| Line 11: | Line 11: | ||
An ''exponential modality'' is an arbitrary (possibly empty) sequence of the two exponential connectives <math>\oc</math> and <math>\wn</math>. It can be considered itself as a unary connective. This leads to the notation <math>\mu A</math> for applying an exponential modality <math>\mu</math> to a formula <math>A</math>. |
An ''exponential modality'' is an arbitrary (possibly empty) sequence of the two exponential connectives <math>\oc</math> and <math>\wn</math>. It can be considered itself as a unary connective. This leads to the notation <math>\mu A</math> for applying an exponential modality <math>\mu</math> to a formula <math>A</math>. |
||
| − | There is a preorder relation on exponential modalities defined by <math>\mu\lesssim\nu</math> if and only if for any formula <math>A</math> we have <math>\mu A\vdash \nu A</math>. It induces an equivalence relation on exponential modalities by <math>\mu \sim \nu</math> if and only if <math>\mu\lesssim\nu</math> and <math>\nu\lesssim\mu</math>. |
+ | There is a preorder relation on exponential modalities defined by <math>\mu\lesssim\nu</math> if and only if for any formula <math>A</math> we have <math>\mu A\vdash \nu A</math>. It induces an [[List of equivalences|equivalence]] relation on exponential modalities by <math>\mu \sim \nu</math> if and only if <math>\mu\lesssim\nu</math> and <math>\nu\lesssim\mu</math>. |
{{Lemma| |
{{Lemma| |
||
Latest revision as of 12:26, 21 November 2014
![\xymatrix{
& & {\wn} \\
& & & & {\wn\oc\wn}\ar[ull] \\
\varepsilon\ar[uurr] & & & {\oc\wn} \ar[ur] & & {\wn\oc} \ar[ul] \\
& & & & {\oc\wn\oc} \ar[ul]\ar[ur] \\
& & {\oc} \ar[uull]\ar[urr]
}](/mediawiki/images/math/e/7/1/e710e498a4904e4aec55029f61ac16da.png)
An exponential modality is an arbitrary (possibly empty) sequence of the two exponential connectives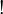 
and 
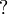. It can be considered itself as a unary connective. This leads to the notation μA for applying an exponential modality μ to a formula A.
There is a preorder relation on exponential modalities defined by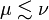 
if and only if for any formula A we have 
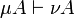. It induces an equivalence relation on exponential modalities by μ˜ν if and only if 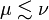and 
.
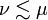Lemma
For any formula A, 
and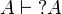 
.
Lemma (Functoriality)
If A and B are two formulas such that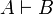 
then, for any exponential modality μ, 
.
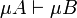Lemma
For any formula A,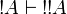 
and 
.
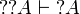Lemma
For any formula A,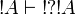 
and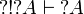 
.
This allows to prove that any exponential modality is equivalent to one of the following seven modalities: 
(the empty modality), , , 
, 
, 
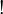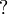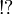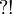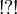or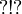 
.
Indeed any sequence of consecutive or 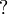in a modality can be simplified into only one occurrence, and then any alternating sequence of length at least four can be simplified into a smaller one.
Proof.
We obtain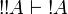 
by functoriality from (and similarly for 
).
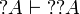From 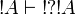, we deduce 
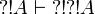by functoriality and 
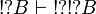(with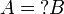 
). In a similar way we have 
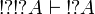and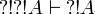 
.
The order relation induced on equivalence classes of exponential modalities with respect to ˜ can be proved to be the one represented on the picture in the top of this page. All the represented relations are valid.
Proof.
We have already seen and 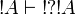. By functoriality we deduce 
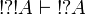and by 
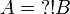we deduce 
.
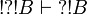The others are obtained from these ones by duality: 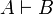entails 
.
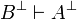Lemma
If α is an atom,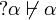 
and
.
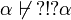We can prove that no other relation between classes is true (by relying on the previous lemma).
Proof.
From the lemma and 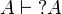, we have 
.
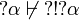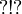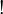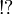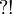Then cannot be smaller than any other of the seven modalities (since they are all smaller than or ). For the same reason, cannot be smaller than , , or 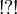. This entails that 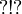is only smaller than 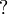since it is not smaller than (by duality from not smaller than ).
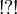From these,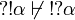 
and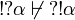 
, we deduce that no other relation is possible.
The order relation on equivalence classes of exponential modalities is a lattice.
