Intuitionistic linear logic
(Definition of ILL and embedding into LL (two-sided presentation)) |
(→The intuitionistic fragment of linear logic: Updated counter-example with 0 only) |
||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Intuitionistic Linear Logic (<math>ILL</math>) is the |
Intuitionistic Linear Logic (<math>ILL</math>) is the |
||
[[intuitionnistic restriction]] of linear logic: the sequent calculus |
[[intuitionnistic restriction]] of linear logic: the sequent calculus |
||
| − | of <math>ILL</math> is obtained from the two-sided sequent calculus of |
+ | of <math>ILL</math> is obtained from the [[Sequent calculus#Sequents and proofs|two-sided sequent calculus of |
| − | linear logic by constraining sequents to have exactly one formula on |
+ | linear logic]] by constraining sequents to have exactly one formula on |
the right-hand side: <math>\Gamma\vdash A</math>. |
the right-hand side: <math>\Gamma\vdash A</math>. |
||
| Line 11: | Line 11: | ||
<math> |
<math> |
||
| − | \LabelRule{\textit{ax}} |
+ | \LabelRule{\rulename{ax}} |
\NulRule{A\vdash A} |
\NulRule{A\vdash A} |
||
\DisplayProof |
\DisplayProof |
||
| Line 17: | Line 17: | ||
\AxRule{\Gamma\vdash A} |
\AxRule{\Gamma\vdash A} |
||
\AxRule{\Delta,A\vdash C} |
\AxRule{\Delta,A\vdash C} |
||
| − | \LabelRule{\textit{cut}} |
+ | \LabelRule{\rulename{cut}} |
\BinRule{\Gamma,\Delta\vdash C} |
\BinRule{\Gamma,\Delta\vdash C} |
||
\DisplayProof |
\DisplayProof |
||
| Line 138: | Line 138: | ||
\AxRule{\Gamma\vdash A} |
\AxRule{\Gamma\vdash A} |
||
\LabelRule{\forall R} |
\LabelRule{\forall R} |
||
| − | \UnaRule{\Gamma\vdash \forall\alpha A} |
+ | \UnaRule{\Gamma\vdash \forall\xi A} |
\DisplayProof |
\DisplayProof |
||
\qquad |
\qquad |
||
| − | \AxRule{\Gamma,A[\tau/\alpha]\vdash C} |
+ | \AxRule{\Gamma,A[\tau/\xi]\vdash C} |
\LabelRule{\forall L} |
\LabelRule{\forall L} |
||
| − | \UnaRule{\Gamma,\forall\alpha A\vdash C} |
+ | \UnaRule{\Gamma,\forall\xi A\vdash C} |
\DisplayProof |
\DisplayProof |
||
\qquad |
\qquad |
||
| − | \AxRule{\Gamma\vdash A[\tau/\alpha]} |
+ | \AxRule{\Gamma\vdash A[\tau/\xi]} |
\LabelRule{\exists R} |
\LabelRule{\exists R} |
||
| − | \UnaRule{\Gamma\vdash\exists\alpha A} |
+ | \UnaRule{\Gamma\vdash\exists\xi A} |
\DisplayProof |
\DisplayProof |
||
\qquad |
\qquad |
||
\AxRule{\Gamma,A\vdash C} |
\AxRule{\Gamma,A\vdash C} |
||
\LabelRule{\exists L} |
\LabelRule{\exists L} |
||
| − | \UnaRule{\Gamma,\exists\alpha A\vdash C} |
+ | \UnaRule{\Gamma,\exists\xi A\vdash C} |
\DisplayProof |
\DisplayProof |
||
</math> |
</math> |
||
| − | with <math>\alpha</math> not free in <math>\Gamma,C</math> in the rules <math>\forall R</math> and <math>\exists L</math>. |
+ | with <math>\xi</math> not free in <math>\Gamma,C</math> in the rules <math>\forall R</math> and <math>\exists L</math>. |
== The intuitionistic fragment of linear logic == |
== The intuitionistic fragment of linear logic == |
||
| Line 164: | Line 164: | ||
<math> |
<math> |
||
| − | J ::= X \mid J\tens J \mid \one \mid J\limp J \mid J\with J \mid \top \mid J\plus J \mid \zero \mid \oc{J} \mid \forall\alpha J \mid \exists\alpha J |
+ | J ::= X \mid J\tens J \mid \one \mid J\limp J \mid J\with J \mid \top \mid J\plus J \mid \zero \mid \oc{J} \mid \forall\xi J \mid \exists\xi J |
</math> |
</math> |
||
<math>JLL</math> is the [[fragment]] of linear logic obtained by restriction to intuitionistic formulas. |
<math>JLL</math> is the [[fragment]] of linear logic obtained by restriction to intuitionistic formulas. |
||
| − | {{Theorem|title=<math>JLL</math> and <math>ILL</math>| |
+ | {{Proposition|title=From <math>ILL</math> to <math>JLL</math>| |
| − | <math>\Gamma\vdash A</math> is provable in <math>ILL_1</math> if and only if it is provable in <math>JLL_1</math>. |
+ | If <math>\Gamma\vdash A</math> is provable in <math>ILL_{012}</math>, it is provable in <math>JLL_{012}</math>. |
}} |
}} |
||
{{Proof| |
{{Proof| |
||
| − | The first direction is immediate since <math>ILL_1</math> is included in <math>JLL_1</math>. |
+ | <math>ILL_{012}</math> is included in <math>JLL_{012}</math>. |
| + | }} |
||
| − | For the second direction, we consider a cut-free proof of <math>\Gamma\vdash A</math> in <math>JLL_1</math>. We prove by induction on the length of such a proof that it belongs to <math>ILL_1</math>. |
+ | {{Theorem|title=From <math>JLL</math> to <math>ILL</math>| |
| + | If <math>\Gamma\vdash\Delta</math> is provable in <math>JLL_{12}</math>, it is provable in <math>ILL_{12}</math>. |
||
}} |
}} |
||
| + | {{Proof| |
||
| + | We only prove the first order case, a proof of the full result is given in the PhD thesis of Harold Schellinx<ref>{{BibEntry|bibtype=phdthesis|author=Schellinx, Harold|title=The Noble Art of Linear Decorating|type=Dissertation series of the Dutch Institute for Logic, Language and Computation|school=University of Amsterdam|note=ILLC-Dissertation Series, 1994-1|year=1994}}</ref>. |
||
| − | This result is still valid with units from <math>ILL_1</math> into <math>JLL_1</math>. In the opposite direction, it holds with <math>\one</math> but not anymore with <math>\top</math> and <math>\zero</math>. <math>{}\vdash((X\limp Y)\limp\zero)\limp(X\tens\top)</math> is provable in <math>JLL_1</math>: |
+ | Consider a cut-free proof of <math>\Gamma\vdash\Delta</math> in <math>JLL_{12}</math>, we can prove by induction on the length of such a proof that it belongs to <math>ILL_{12}</math>. |
| + | }} |
||
| + | |||
| + | {{Corollary|title=Unique conclusion in <math>JLL</math>| |
||
| + | If <math>\Gamma\vdash\Delta</math> is provable in <math>JLL_{12}</math> then <math>\Delta</math> is a singleton. |
||
| + | }} |
||
| + | |||
| + | The theorem is also valid for formulas containing <math>\one</math> or <math>\top</math> but not anymore with <math>\zero</math>. <math>{}\vdash((X\limp Y)\limp\zero)\limp(X\tens(\zero\limp Z))</math> is provable in <math>JLL_0</math>: |
||
<math> |
<math> |
||
| − | \LabelRule{\textit{ax}} |
+ | \LabelRule{\rulename{ax}} |
\NulRule{X\vdash X} |
\NulRule{X\vdash X} |
||
| − | \LabelRule{\top R} |
+ | \LabelRule{\zero L} |
| − | \NulRule{{}\vdash Y,\top} |
+ | \NulRule{\zero\vdash Y,Z} |
| + | \LabelRule{\limp R} |
||
| + | \UnaRule{{}\vdash Y,\zero\limp Z} |
||
\LabelRule{\tens R} |
\LabelRule{\tens R} |
||
| − | \BinRule{X\vdash Y,X\tens\top} |
+ | \BinRule{X\vdash Y,X\tens(\zero\limp Z)} |
\LabelRule{\limp R} |
\LabelRule{\limp R} |
||
| − | \UnaRule{{}\vdash X\limp Y,X\tens\top} |
+ | \UnaRule{{}\vdash X\limp Y,X\tens(\zero\limp Z)} |
\LabelRule{\zero L} |
\LabelRule{\zero L} |
||
\NulRule{\zero\vdash {}} |
\NulRule{\zero\vdash {}} |
||
\LabelRule{\limp L} |
\LabelRule{\limp L} |
||
| − | \BinRule{(X\limp Y)\limp\zero\vdash X\tens\top} |
+ | \BinRule{(X\limp Y)\limp\zero\vdash X\tens(\zero\limp Z)} |
\LabelRule{\limp R} |
\LabelRule{\limp R} |
||
| − | \UnaRule{{}\vdash((X\limp Y)\limp\zero)\limp(X\tens\top)} |
+ | \UnaRule{{}\vdash((X\limp Y)\limp\zero)\limp(X\tens(\zero\limp Z))} |
\DisplayProof |
\DisplayProof |
||
</math> |
</math> |
||
| − | but not in <math>ILL_1</math>. |
+ | but not in <math>ILL_0</math>. |
| + | |||
| + | == Input / output polarities == |
||
| + | |||
| + | In order to go to <math>LL</math> without <math>\limp</math>, we consider two classes of formulas: ''input formulas'' (<math>I</math>) and ''output formulas'' (<math>O</math>). |
||
| + | |||
| + | <math> |
||
| + | I ::= X\orth \mid I\parr I \mid \bot \mid I\tens O \mid O\tens I \mid I\plus I \mid \zero \mid I\with I \mid \top \mid \wn{I} \mid \exists\xi I \mid \forall\xi I |
||
| + | </math> |
||
| + | <math> |
||
| + | O ::= X \mid O\tens O \mid \one \mid O\parr I \mid I\parr O \mid O\with O \mid \top \mid O\plus O \mid \zero \mid \oc{O} \mid \forall\xi O \mid \exists\xi O |
||
| + | </math> |
||
| + | |||
| + | By applying the definition of the linear implication <math>A\limp B = A\orth\parr B</math>, any formula of <math>JLL</math> is mapped to an output formula (and the dual of a <math>JLL</math> formula to an input formula). Conversely, any output formula is coming from a <math>JLL</math> formula in this way (up to commutativity of <math>\parr</math>: <math>O\parr I = I\parr O</math>). |
||
| + | |||
| + | The [[fragment]] of linear logic obtained by restriction to input/output formulas is thus equivalent to <math>JLL</math>, but the closure of the set of input/output formulas under orthogonal allows for a one-sided presentation. |
||
| + | |||
| + | <math> |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{\vdash O\orth,O} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash \Gamma,O} |
||
| + | \AxRule{{}\vdash\Delta,O\orth} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{{}\vdash\Gamma,\Delta} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{{}\vdash\Gamma,A} |
||
| + | \AxRule{{}\vdash\Delta,B} |
||
| + | \LabelRule{\tens} |
||
| + | \BinRule{{}\vdash\Gamma,\Delta,A\tens B} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma,A,B} |
||
| + | \LabelRule{\parr} |
||
| + | \UnaRule{{}\vdash\Gamma,A\parr B} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \LabelRule{\one} |
||
| + | \NulRule{{}\vdash\one} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma} |
||
| + | \LabelRule{\bot} |
||
| + | \UnaRule{{}\vdash\Gamma,\bot} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{{}\vdash\Gamma,A} |
||
| + | \AxRule{{}\vdash\Gamma,B} |
||
| + | \LabelRule{\with} |
||
| + | \BinRule{{}\vdash\Gamma,A\with B} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma,A} |
||
| + | \LabelRule{\plus_1} |
||
| + | \UnaRule{{}\vdash\Gamma,A\plus B} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma,B} |
||
| + | \LabelRule{\plus_2} |
||
| + | \UnaRule{{}\vdash\Gamma,A\plus B} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \LabelRule{\top} |
||
| + | \NulRule{{}\vdash\Gamma,\top} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{{}\vdash\wn{\Gamma},O} |
||
| + | \LabelRule{\oc} |
||
| + | \UnaRule{{}\vdash\wn{\Gamma},\oc{O}} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma,I} |
||
| + | \LabelRule{\wn d} |
||
| + | \UnaRule{{}\vdash\Gamma,\wn{I}} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma,\wn{I},\wn{I}} |
||
| + | \LabelRule{\wn c} |
||
| + | \UnaRule{{}\vdash\Gamma,\wn{I}} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma} |
||
| + | \LabelRule{\wn w} |
||
| + | \UnaRule{{}\vdash\Gamma,\wn{I}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{{}\vdash\Gamma,A} |
||
| + | \LabelRule{\forall} |
||
| + | \UnaRule{{}\vdash\Gamma,\forall\xi A} |
||
| + | \DisplayProof |
||
| + | \qquad |
||
| + | \AxRule{{}\vdash\Gamma,A[\tau/\xi]} |
||
| + | \LabelRule{\exists} |
||
| + | \UnaRule{{}\vdash\Gamma,\exists\xi A} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | with <math>A</math> and <math>B</math> arbitrary input or output formulas (under the condition that the composite formulas containing them are input or output formulas) and <math>\xi</math> not free in <math>\Gamma</math> in the rule <math>\forall</math>. |
||
| + | |||
| + | {{Lemma|title=Output formula| |
||
| + | If <math>{}\vdash\Gamma</math> is provable in <math>LL_{12}</math> and contains only input and output formulas, then <math>\Gamma</math> contains exactly one output formula. |
||
| + | }} |
||
| + | |||
| + | {{Proof| |
||
| + | Assume <math>\Gamma_O</math> is obtained by turning the output formulas of <math>\Gamma</math> into <math>JLL</math> formulas and <math>\Gamma_I</math> is obtained by turning the dual of the input formulas of <math>\Gamma</math> into <math>JLL</math> formulas, <math>\Gamma_I\vdash\Gamma_O</math> is provable in <math>LL_{12}</math> thus in <math>JLL_{12}</math>. By corollary (Unique conclusion in <math>JLL</math>), <math>\Gamma_O</math> is a singleton, thus <math>\Gamma</math> contains exactly one output formula. |
||
| + | }} |
||
| + | |||
| + | == References == |
||
| + | <references /> |
||
Latest revision as of 10:31, 13 March 2017
Intuitionistic Linear Logic (ILL) is the
intuitionnistic restriction of linear logic: the sequent calculus
of ILL is obtained from the two-sided sequent calculus of
linear logic by constraining sequents to have exactly one formula on
the right-hand side: 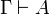 .
.
The connectives 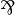 ,
, 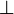 and
and 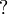 are
not available anymore, but the linear implication
are
not available anymore, but the linear implication 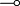 is.
is.
Contents |
[edit] Sequent Calculus
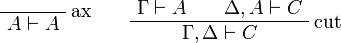
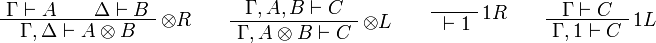
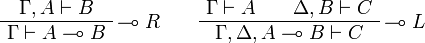
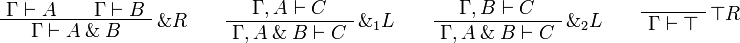
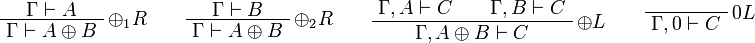
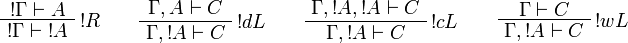
![\AxRule{\Gamma\vdash A}
\LabelRule{\forall R}
\UnaRule{\Gamma\vdash \forall\xi A}
\DisplayProof
\qquad
\AxRule{\Gamma,A[\tau/\xi]\vdash C}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\xi A\vdash C}
\DisplayProof
\qquad
\AxRule{\Gamma\vdash A[\tau/\xi]}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash\exists\xi A}
\DisplayProof
\qquad
\AxRule{\Gamma,A\vdash C}
\LabelRule{\exists L}
\UnaRule{\Gamma,\exists\xi A\vdash C}
\DisplayProof](/mediawiki/images/math/c/9/4/c9406bb4faaab1b352071a9aa9dbf5d8.png)
with ξ not free in Γ,C in the rules 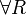 and
and 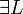 .
.
[edit] The intuitionistic fragment of linear logic
In order to characterize intuitionistic linear logic inside linear logic, we define the intuitionistic restriction of linear formulas:
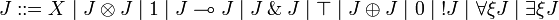
JLL is the fragment of linear logic obtained by restriction to intuitionistic formulas.
Proposition (From ILL to JLL)
If 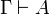 is provable in ILL012, it is provable in JLL012.
is provable in ILL012, it is provable in JLL012.
Proof. ILL012 is included in JLL012.
Theorem (From JLL to ILL)
If 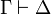 is provable in JLL12, it is provable in ILL12.
is provable in JLL12, it is provable in ILL12.
Proof. We only prove the first order case, a proof of the full result is given in the PhD thesis of Harold Schellinx[1].
Consider a cut-free proof of 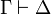 in JLL12, we can prove by induction on the length of such a proof that it belongs to ILL12.
in JLL12, we can prove by induction on the length of such a proof that it belongs to ILL12.
Corollary (Unique conclusion in JLL)
If 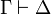 is provable in JLL12 then Δ is a singleton.
is provable in JLL12 then Δ is a singleton.
The theorem is also valid for formulas containing 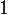 or
or 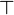 but not anymore with
but not anymore with 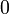 .
. 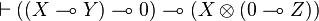 is provable in JLL0:
is provable in JLL0:
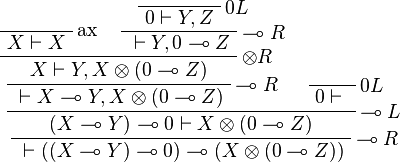
but not in ILL0.
[edit] Input / output polarities
In order to go to LL without 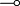 , we consider two classes of formulas: input formulas (I) and output formulas (O).
, we consider two classes of formulas: input formulas (I) and output formulas (O).
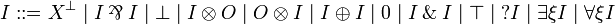
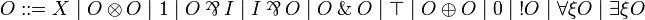
By applying the definition of the linear implication 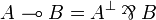 , any formula of JLL is mapped to an output formula (and the dual of a JLL formula to an input formula). Conversely, any output formula is coming from a JLL formula in this way (up to commutativity of
, any formula of JLL is mapped to an output formula (and the dual of a JLL formula to an input formula). Conversely, any output formula is coming from a JLL formula in this way (up to commutativity of 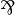 :
: 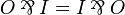 ).
).
The fragment of linear logic obtained by restriction to input/output formulas is thus equivalent to JLL, but the closure of the set of input/output formulas under orthogonal allows for a one-sided presentation.
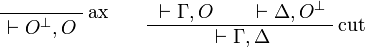
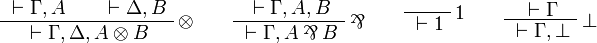
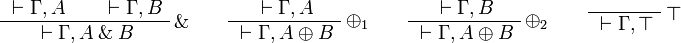
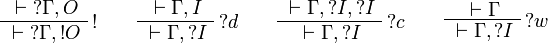
![\AxRule{{}\vdash\Gamma,A}
\LabelRule{\forall}
\UnaRule{{}\vdash\Gamma,\forall\xi A}
\DisplayProof
\qquad
\AxRule{{}\vdash\Gamma,A[\tau/\xi]}
\LabelRule{\exists}
\UnaRule{{}\vdash\Gamma,\exists\xi A}
\DisplayProof](/mediawiki/images/math/b/6/d/b6d7bca46377ab6c01b8c59e0488556e.png)
with A and B arbitrary input or output formulas (under the condition that the composite formulas containing them are input or output formulas) and ξ not free in Γ in the rule 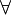 .
.
Lemma (Output formula)
If 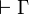 is provable in LL12 and contains only input and output formulas, then Γ contains exactly one output formula.
is provable in LL12 and contains only input and output formulas, then Γ contains exactly one output formula.
Proof.
Assume ΓO is obtained by turning the output formulas of Γ into JLL formulas and ΓI is obtained by turning the dual of the input formulas of Γ into JLL formulas, 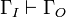 is provable in LL12 thus in JLL12. By corollary (Unique conclusion in JLL), ΓO is a singleton, thus Γ contains exactly one output formula.
is provable in LL12 thus in JLL12. By corollary (Unique conclusion in JLL), ΓO is a singleton, thus Γ contains exactly one output formula.
[edit] References
- ↑ Schellinx, Harold. The Noble Art of Linear Decorating. Dissertation series of the Dutch Institute for Logic, Language and Computation. University of Amsterdam. ILLC-Dissertation Series, 1994-1, 1994.