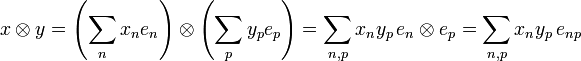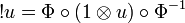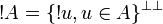GoI for MELL: exponentials
m (style) |
(definition of type !A) |
||
| Line 21: | Line 21: | ||
Being both separable Hilbert spaces, <math>H</math> and <math>H\tens H</math> are isomorphic. We will now define explicitely an iso based on partial permutations. |
Being both separable Hilbert spaces, <math>H</math> and <math>H\tens H</math> are isomorphic. We will now define explicitely an iso based on partial permutations. |
||
| − | We fix, once for all, a bijection from couples of natural numbers to natural numbers that we will denote by <math>(n,p)\mapsto\langle n,p\rangle</math>. For example set <math>\langle n,p\rangle = 2^n(2p+1) - 1</math>. |
+ | We fix, once for all, a bijection from couples of natural numbers to natural |
| + | numbers that we will denote by <math>(n,p)\mapsto\langle n,p\rangle</math>. For |
||
| + | example set <math>\langle n,p\rangle = 2^n(2p+1) - 1</math>. Conversely, given |
||
| + | <math>n\in\mathbb{N}</math> we denote by <math>n_{(1)}</math> and |
||
| + | <math>n_{(2)}</math> the unique integers such that <math>\langle n_{(1)}, |
||
| + | n_{(2)}\rangle = n</math>. |
||
{{Remark| |
{{Remark| |
||
| Line 51: | Line 51: | ||
If we suppose that <math>u = u_\varphi</math> is a <math>p</math>-isometry generated by the partial permutation <math>\varphi</math> then we have: |
If we suppose that <math>u = u_\varphi</math> is a <math>p</math>-isometry generated by the partial permutation <math>\varphi</math> then we have: |
||
: <math>!u(e_{\langle n,p\rangle}) = \Phi(e_n\tens u(e_p)) = \Phi(e_n\tens e_{\varphi(p)}) = e_{\langle n,\varphi(p)\rangle}</math>. |
: <math>!u(e_{\langle n,p\rangle}) = \Phi(e_n\tens u(e_p)) = \Phi(e_n\tens e_{\varphi(p)}) = e_{\langle n,\varphi(p)\rangle}</math>. |
||
| − | Thus <math>!u</math> is itself a <math>p</math>-isometry and the proof space is stable under the copying iso. |
+ | Thus <math>!u_\varphi</math> is itself a <math>p</math>-isometry generated by the |
| + | partial permutation <math>!\varphi:n\mapsto \langle n_{(1)}, \varphi(n_{(2)})\rangle</math>, which shows that the proof space is stable under the copying iso. |
||
| + | |||
| + | Given a type <math>A</math> we define the type <math>!A</math> by: |
||
| + | : <math>!A = \{!u, u\in A\}\biorth</math> |
||
Latest revision as of 13:29, 17 November 2010
[edit] The tensor product of Hilbert spaces
Recall that we work in the Hilbert space 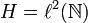 endowed with its canonical hilbertian basis denoted by
endowed with its canonical hilbertian basis denoted by 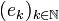 .
.
The space 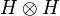 is the collection of sequences
is the collection of sequences 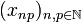 of complex numbers such that
of complex numbers such that
| ∑ | | xnp | 2 |
| n,p |
converges. The scalar product is defined just as before:
-
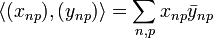 .
.
If 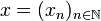 and
and 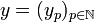 are vectors in H then their tensor is the sequence:
are vectors in H then their tensor is the sequence:
-
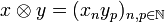 .
.
We define: 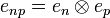 so that enp is the sequence
so that enp is the sequence 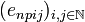 of complex numbers given by enpij = δniδpj. By bilinearity of tensor we have:
of complex numbers given by enpij = δniδpj. By bilinearity of tensor we have:
Furthermore the system of vectors (enp) is a hilbertian basis of 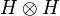 : the sequence
: the sequence 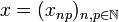 may be written:
may be written:
-
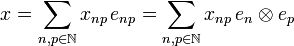 .
.
[edit] An algebra isomorphism
Being both separable Hilbert spaces, H and 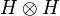 are isomorphic. We will now define explicitely an iso based on partial permutations.
are isomorphic. We will now define explicitely an iso based on partial permutations.
We fix, once for all, a bijection from couples of natural numbers to natural
numbers that we will denote by 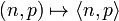 . For
example set
. For
example set 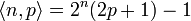 . Conversely, given
. Conversely, given
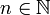 we denote by n(1) and
n(2) the unique integers such that
we denote by n(1) and
n(2) the unique integers such that 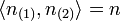 .
.
Remark:
just as it was convenient but actually not necessary to choose p and q so that pp * + qq * = 1 it is actually not necessary to have a bijection, a one-to-one mapping from 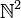 into
into 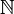 would be sufficient for our purpose.
would be sufficient for our purpose.
This bijection can be extended into a Hilbert space isomorphism 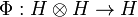 by defining:
by defining:
-
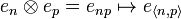 .
.
Now given an operator u on H we define the operator !u on H by:
-
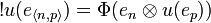 .
.
Remark: The operator !u is defined by:
where 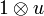 denotes the operator on
denotes the operator on 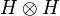 defined by
defined by 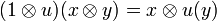 for any x,y in H. However this notation must not be confused with the tensor of operators that was defined in the previous section in order to interpret the tensor rule of linear logic; we therefore will not use it.
for any x,y in H. However this notation must not be confused with the tensor of operators that was defined in the previous section in order to interpret the tensor rule of linear logic; we therefore will not use it.
One can check that given two operators u and v we have:
- !u!v = !(uv);
- !(u * ) = (!u) * .
Due to the fact that Φ is an isomorphism onto we also have !1 = 1; this however will not be used.
We therefore have that ! is a morphism on 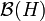 ; it is easily seen to be an iso (not onto though). As this is the crucial ingredient for interpreting the structural rules of linear logic, we will call it the copying iso.
; it is easily seen to be an iso (not onto though). As this is the crucial ingredient for interpreting the structural rules of linear logic, we will call it the copying iso.
[edit] Interpretation of exponentials
If we suppose that 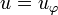 is a p-isometry generated by the partial permutation
is a p-isometry generated by the partial permutation 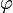 then we have:
then we have:
-
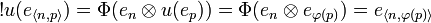 .
.
Thus 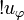 is itself a p-isometry generated by the
partial permutation
is itself a p-isometry generated by the
partial permutation 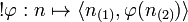 , which shows that the proof space is stable under the copying iso.
, which shows that the proof space is stable under the copying iso.
Given a type A we define the type !A by: