Geometry of interaction
The geometry of interaction, GoI in short, was defined in the early nineties by Girard as an interpretation of linear logic into operators algebra: formulae were interpreted by Hilbert spaces and proofs by partial isometries. This was a striking novelty as it was the first time that a mathematical model of logic (lambda-calculus) didn't interpret a proof of  as a morphism from (the space interpreting) A to the (space interpreting) B and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on (the space interpreting)
as a morphism from (the space interpreting) A to the (space interpreting) B and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on (the space interpreting)  , that is a morphism from
, that is a morphism from  to
to  . For proof composition the problem was then, given an operator on
. For proof composition the problem was then, given an operator on  and another one on
and another one on 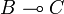 to construct a new operator on
to construct a new operator on 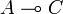 . This problem was originally expressed as a feedback equation solved by the execution formula. The fact that the execution formula has some formal analogies with Kleene's formula for recursive functions allowed to claim that GoI was an operational semantics, as opposed to traditionnal denotational semantics.
. This problem was originally expressed as a feedback equation solved by the execution formula. The fact that the execution formula has some formal analogies with Kleene's formula for recursive functions allowed to claim that GoI was an operational semantics, as opposed to traditionnal denotational semantics.
The first instance of the GoI was restricted to the MELL fragment of linear logic (Multiplicative and Exponential fragment) which is enough to encode lambda-calculus. Since then Girard proposed several improvements: firstly the extension to the additive connectives known as Geometry of Interaction 3 and more recently a complete reformulation using Von Neumann algebras that allows to deal with some aspects of implicit complexity
The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; in particular the execution formula appears as the composition of two automata that interact one with the other through their common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the MELL fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal.