Geometry of interaction
m (typos, style) |
(Started the description of GoI as operators on Hilbert space) |
||
| Line 6: | Line 6: | ||
The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; in particular the execution formula appears as the composition of two automata that interact one with the other through their common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the <math>MELL</math> fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal. |
The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; in particular the execution formula appears as the composition of two automata that interact one with the other through their common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the <math>MELL</math> fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal. |
||
| + | |||
| + | = The Geometry of Interaction as an abstract machine = |
||
| + | |||
| + | = The Geometry of Interaction as operators = |
||
| + | |||
| + | The original construction of GoI by Girard follows a general pattern already mentionned in [[coherent semantics]] under the name ''symmetric reducibility''. First set a general space; here, in the case of GoI, the space will be the space of bounded operators on <math>H=\ell^2(\mathbb{C})</math>. This is where the interpretations of proof objects will live. Second define a suitable duality on the space that will be denoted as <math>u\perp v</math>. For the GoI, two dualities have proved to work, the first one being nilpotency: two operators <math>u</math> and <math>v</math> are dual if <math>uv</math> is nilpotent, that is, if there is an nonegative integer <math>n</math> such that <math>(uv)^n = 0</math>. Last define a ''type'' as a set of objects <math>T</math> that is equal to its bidual: <math>T = T\biorth</math>. Putting it in ground terms this means that <math>u\in T</math> iff for all operator <math>v</math>, if <math>v\in T\orth</math>, that is if <math>u'v</math> is nilpotent for all <math>u'\in T</math>, then <math>u\perp v</math>, that is <math>uv</math> is nilpotent. |
||
| + | |||
| + | It remains to interpret logical operations in this framework, that is to associate a type to each formula, an object to each proof and to show the adequacy lemma: if <math>u</math> is the interpretation of a proof of the formula <math>A</math> then <math>u</math> belongs to the type associated to <math>A</math>. |
||
| + | |||
| + | == Preliminaries == |
||
| + | |||
| + | We begin by a brief tour of the operations on <math>H</math> that will be used in the sequel. |
||
| + | |||
| + | Let us denote by <math>(e_n)_{n\in\mathbb{N}}</math> the canonical hilbertian basis of <math>H = \ell^2</math>; <math>e_n</math> is the sequence containing only 0's but at the <math>n</math>'s position where its value is <math>1</math>: <math>e_n = (\delta_{in})_{i\in\mathbb{N}}</math> where <math>\delta_{in}</math> is the standard Kroenecker function. Recall that the adjoint of an operator <math>u</math> is the operator <math>u^\ast</math> defined by <math>\langle u(x), y\rangle = \langle x, u^\ast(y)\rangle</math> for any <math>x,y\in H</math>. |
||
| + | |||
| + | A ''partial isometry'' is an operator <math>u</math> satisfying <math>uu^\ast u = u</math>; as a consequence <math>uu^\ast</math> is a projector the range of which is the range of <math>u</math>; we will call ''codomain'' the range of <math>u</math>. Similarly <math>u^\ast u</math> is also a projector the range of which is the ''domain'' of <math>u</math> (which is orthogonal to the kernel of <math>u</math>). The domain and the codomain of <math>u</math> are both closed subspace of <math>H</math> and <math>u</math> restricted to its domain is an isometry. If the domain <math>u</math> is <math>H</math> that is if <math>u^\ast u = 1</math> we say that <math>u</math> has ''full domain'', and similarly for codomain. |
||
| + | |||
| + | If <math>u</math> is a partial isometry then <math>u^\ast</math> is also a partial isometry the domain of which is the codomain of <math>u</math> and the codomain of which is the domain of <math>u</math>. |
||
| + | |||
| + | If <math>u</math> and <math>v</math> are two partial isometries, the equation <math>uu^\ast + vv^\ast = 1</math> means that the codomains of <math>u</math> and <math>v</math> are orthogonal and that their direct sum is <math>H</math>. |
||
| + | |||
| + | We shall define a number of operators on <math>H</math> by describing their action on the basis <math>(e_n)</math>; actually most of the operators that are used to interpret logical operations will turn out to be defined as partial permutations on the basis, which in particular entails that they are partial isometries. |
||
| + | |||
| + | == Interpreting the tensor == |
||
| + | |||
| + | The first step is, given two types <math>A</math> and <math>B</math>, to construct the type <math>A\tens B</math>. For this purpose we will define an isomorphism <math>H\oplus H \cong H</math> by <math>x\oplus y\rightsquigarrow p(x)+q(y)</math> where <math>p:H\mapsto H</math> and <math>q:H\mapsto H</math> are given by: |
||
| + | |||
| + | : <math>p(e_n) = e_{2n}</math>, |
||
| + | : <math>q(e_n) = e_{2n+1}</math>. |
||
| + | |||
| + | This is actually arbitrary, any two partial isometries <math>p,q</math> with full domain and such that the sum of their codomains is <math>H</math> would do the job. |
||
Revision as of 22:03, 27 March 2010
The geometry of interaction, GoI in short, was defined in the early nineties by Girard as an interpretation of linear logic into operators algebra: formulae were interpreted by Hilbert spaces and proofs by partial isometries.
This was a striking novelty as it was the first time that a mathematical model of logic (lambda-calculus) didn't interpret a proof of 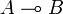 as a morphism from (the space interpreting) A to (the space interpreting) B and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on (the space interpreting)
as a morphism from (the space interpreting) A to (the space interpreting) B and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on (the space interpreting) 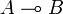 , that is a morphism from
, that is a morphism from 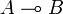 to
to  . For proof composition the problem was then, given an operator on
. For proof composition the problem was then, given an operator on 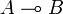 and another one on
and another one on 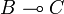 to construct a new operator on
to construct a new operator on 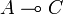 . This problem was originally expressed as a feedback equation solved by the execution formula. The execution formula has some formal analogies with Kleene's formula for recursive functions, which allowed to claim that GoI was an operational semantics, as opposed to traditionnal denotational semantics.
. This problem was originally expressed as a feedback equation solved by the execution formula. The execution formula has some formal analogies with Kleene's formula for recursive functions, which allowed to claim that GoI was an operational semantics, as opposed to traditionnal denotational semantics.
The first instance of the GoI was restricted to the MELL fragment of linear logic (Multiplicative and Exponential fragment) which is enough to encode lambda-calculus. Since then Girard proposed several improvements: firstly the extension to the additive connectives known as Geometry of Interaction 3 and more recently a complete reformulation using Von Neumann algebras that allows to deal with some aspects of implicit complexity
The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; in particular the execution formula appears as the composition of two automata that interact one with the other through their common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the MELL fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal.
Contents |
The Geometry of Interaction as an abstract machine
The Geometry of Interaction as operators
The original construction of GoI by Girard follows a general pattern already mentionned in coherent semantics under the name symmetric reducibility. First set a general space; here, in the case of GoI, the space will be the space of bounded operators on 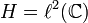 . This is where the interpretations of proof objects will live. Second define a suitable duality on the space that will be denoted as
. This is where the interpretations of proof objects will live. Second define a suitable duality on the space that will be denoted as 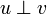 . For the GoI, two dualities have proved to work, the first one being nilpotency: two operators u and v are dual if uv is nilpotent, that is, if there is an nonegative integer n such that (uv)n = 0. Last define a type as a set of objects T that is equal to its bidual:
. For the GoI, two dualities have proved to work, the first one being nilpotency: two operators u and v are dual if uv is nilpotent, that is, if there is an nonegative integer n such that (uv)n = 0. Last define a type as a set of objects T that is equal to its bidual: 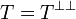 . Putting it in ground terms this means that
. Putting it in ground terms this means that 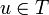 iff for all operator v, if
iff for all operator v, if 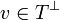 , that is if u'v is nilpotent for all
, that is if u'v is nilpotent for all 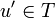 , then
, then 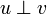 , that is uv is nilpotent.
, that is uv is nilpotent.
It remains to interpret logical operations in this framework, that is to associate a type to each formula, an object to each proof and to show the adequacy lemma: if u is the interpretation of a proof of the formula A then u belongs to the type associated to A.
Preliminaries
We begin by a brief tour of the operations on H that will be used in the sequel.
Let us denote by 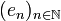 the canonical hilbertian basis of
the canonical hilbertian basis of 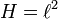 ; en is the sequence containing only 0's but at the n's position where its value is 1:
; en is the sequence containing only 0's but at the n's position where its value is 1: 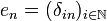 where δin is the standard Kroenecker function. Recall that the adjoint of an operator u is the operator
where δin is the standard Kroenecker function. Recall that the adjoint of an operator u is the operator 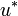 defined by
defined by 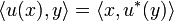 for any
for any 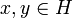 .
.
A partial isometry is an operator u satisfying 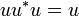 ; as a consequence
; as a consequence 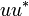 is a projector the range of which is the range of u; we will call codomain the range of u. Similarly
is a projector the range of which is the range of u; we will call codomain the range of u. Similarly 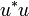 is also a projector the range of which is the domain of u (which is orthogonal to the kernel of u). The domain and the codomain of u are both closed subspace of H and u restricted to its domain is an isometry. If the domain u is H that is if
is also a projector the range of which is the domain of u (which is orthogonal to the kernel of u). The domain and the codomain of u are both closed subspace of H and u restricted to its domain is an isometry. If the domain u is H that is if 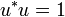 we say that u has full domain, and similarly for codomain.
we say that u has full domain, and similarly for codomain.
If u is a partial isometry then 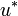 is also a partial isometry the domain of which is the codomain of u and the codomain of which is the domain of u.
is also a partial isometry the domain of which is the codomain of u and the codomain of which is the domain of u.
If u and v are two partial isometries, the equation 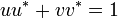 means that the codomains of u and v are orthogonal and that their direct sum is H.
means that the codomains of u and v are orthogonal and that their direct sum is H.
We shall define a number of operators on H by describing their action on the basis (en); actually most of the operators that are used to interpret logical operations will turn out to be defined as partial permutations on the basis, which in particular entails that they are partial isometries.
Interpreting the tensor
The first step is, given two types A and B, to construct the type 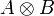 . For this purpose we will define an isomorphism
. For this purpose we will define an isomorphism 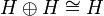 by
by 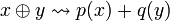 where
where 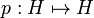 and
and 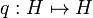 are given by:
are given by:
- p(en) = e2n,
- q(en) = e2n + 1.
This is actually arbitrary, any two partial isometries p,q with full domain and such that the sum of their codomains is H would do the job.