Geometry of interaction
m (style) |
m (ortho) |
||
| (35 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
The ''geometry of interaction'', GoI in short, was defined in the early nineties by Girard as an interpretation of linear logic into operators algebra: formulae were interpreted by Hilbert spaces and proofs by partial isometries. |
The ''geometry of interaction'', GoI in short, was defined in the early nineties by Girard as an interpretation of linear logic into operators algebra: formulae were interpreted by Hilbert spaces and proofs by partial isometries. |
||
| − | This was a striking novelty as it was the first time that a mathematical model of logic (lambda-calculus) didn't interpret a proof of <math>A\limp B</math> as a morphism ''from'' <math>A</math> ''to'' <math>B</math><ref>to be precise one should say from ''the space interpreting'' <math>A</math> to the space interpreting'' <math>B</math></ref>, and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting ''on'' <math>A\limp B</math>, that is a morphism from <math>A\limp B</math> to <math>A\limp B</math>. For proof composition the problem was then, given an operator on <math>A\limp B</math> and another one on <math>B\limp C</math> to construct a new operator on <math>A\limp C</math>. This problem was solved by the ''execution formula'' that bares some formal analogies with Kleene's formula for recursive functions. For this reason GoI was claimed to be an ''operational semantics'', as opposed to traditionnal [[Semantics|denotational semantics]]. |
+ | This was a striking novelty as it was the first time that a mathematical model of logic (lambda-calculus) didn't interpret a proof of <math>A\limp B</math> as a morphism ''from'' <math>A</math> ''to'' <math>B</math> and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting ''on'' <math>A\limp B</math>, that is a morphism from <math>A\limp B</math> to <math>A\limp B</math>. For proof composition the problem was then, given an operator on <math>A\limp B</math> and another one on <math>B\limp C</math> to construct a new operator on <math>A\limp C</math>. This problem was solved by the ''execution formula'' that bares some formal analogies with Kleene's formula for recursive functions. For this reason GoI was claimed to be an ''operational semantics'', as opposed to traditionnal [[Semantics|denotational semantics]]. |
The first instance of the GoI was restricted to the <math>MELL</math> fragment of linear logic (Multiplicative and Exponential fragment) which is enough to encode lambda-calculus. Since then Girard proposed several improvements: firstly the extension to the additive connectives known as ''Geometry of Interaction 3'' and more recently a complete reformulation using Von Neumann algebras that allows to deal with some aspects of [[Light linear logics|implicit complexity]] |
The first instance of the GoI was restricted to the <math>MELL</math> fragment of linear logic (Multiplicative and Exponential fragment) which is enough to encode lambda-calculus. Since then Girard proposed several improvements: firstly the extension to the additive connectives known as ''Geometry of Interaction 3'' and more recently a complete reformulation using Von Neumann algebras that allows to deal with some aspects of [[Light linear logics|implicit complexity]] |
||
| − | The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; in particular the execution formula appears as the composition of two automata that interact one with the other through their common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the <math>MELL</math> fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal. |
+ | The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; the execution formula appears as the composition of two automata interacting through a common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the <math>MELL</math> fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal. |
= The Geometry of Interaction as operators = |
= The Geometry of Interaction as operators = |
||
| − | The original construction of GoI by Girard follows a general pattern already mentionned in [[coherent semantics]] under the name ''symmetric reducibility''. First set a general space called the ''proof space'' because this is where the interpretations of proofs will live. In the case of GoI, the proof space is the space of bounded operators on <math>\ell^2</math>. Note that the proof space generally contains much more objects than interpretations of proofs; in the GoI case we will see that interpretations of proofs happen to be some very peculiar kind of partial isometries. |
+ | The original construction of GoI by Girard follows a general pattern already mentionned in the section on [[coherent semantics]] under the name ''symmetric reducibility'' and that was first put to use in [[phase semantics]]. First set a general space <math>P</math> called the ''proof space'' because this is where the interpretations of proofs will live. Make sure that <math>P</math> is a (not necessarily commutative) monoid. In the case of GoI, the proof space is a subset of the space of bounded operators on <math>\ell^2</math>. |
| − | Second define a duality on this space that will be denoted as <math>u\perp v</math>. For the GoI, two dualities have proved to work, the first one being nilpotency: two operators <math>u</math> and <math>v</math> are dual if <math>uv</math> is nilpotent, that is, if there is a nonegative integer <math>n</math> such that <math>(uv)^n = 0</math>. We will denote by <math>\bot</math> the set of nilpotent operators so that the duality reads: |
+ | Second define a particular subset of <math>P</math> that will be denoted by <math>\bot</math>; then derive a duality on <math>P</math>: for <math>u,v\in P</math>, <math>u</math> and <math>v</math> are dual<ref>In modern terms one says that <math>u</math> and <math>v</math> are ''polar''.</ref>iff <math>uv\in\bot</math>. |
| − | : <math>u\perp v</math> iff <math>uv\in\bot</math>. |
||
| − | This duality applies to operators and shouldn't be confused with orthogonality of vectors. In this article we will use the notation <math>\perp</math> exclusively for the duality of operators. |
+ | Such a duality defines an [[orthogonality relation]], with the usual derived definitions and properties. |
| − | Last define a ''type'' as a subset <math>T</math> of the proof space that is equal to its bidual: <math>T = T\biorth</math>. This means that <math>u\in T</math> iff for all operator <math>v</math>, if <math>v\in T\orth</math>, that is if <math>u'v\in\bot</math> for all <math>u'\in T</math>, then <math>uv\in\bot</math>. |
+ | For the GoI, two dualities have proved to work; we will consider the first one: nilpotency, ''ie'', <math>\bot</math> is the set of nilpotent operators in <math>P</math>. Let us explicit this: two operators <math>u</math> and <math>v</math> are dual if there is a nonnegative integer <math>n</math> such that <math>(uv)^n = 0</math>. This duality is symmetric: if <math>uv</math> is nilpotent then <math>vu</math> is nilpotent also. |
| − | It remains now to interpret logical operations, that is associate a type to each formula, an object to each proof and show the ''adequacy lemma'': if <math>u</math> is the interpretation of a proof of the formula <math>A</math> then <math>u</math> belongs to the type associated to <math>A</math>. |
+ | Last define a ''type'' as a subset <math>T</math> of the proof space that is equal to its bidual: <math>T = T\biorth</math>. This means that <math>u\in T</math> iff for all operator <math>v\in T\orth</math>, that is such that <math>u'v\in\bot</math> for all <math>u'\in T</math>, we have <math>uv\in\bot</math>. |
| − | == Preliminaries == |
+ | The real work<ref>The difficulty is to find the right duality that will make logical operations interpretable. General conditions that allows to achieve this have been formulated by Hyland and Schalk thanks to their theory of ''[[double glueing]]''.</ref>is now to interpret logical operations, that is to associate a type to each formula, an object to each proof and show the ''adequacy lemma'': if <math>u</math> is the interpretation of a proof of the formula <math>A</math> then <math>u</math> belongs to the type associated to <math>A</math>. |
| − | We begin by a brief tour of the operations in Hilbert spaces that will be used in the sequel. In this article <math>H</math> will stand for the Hilbert space <math>\ell^2(\mathbb{N})</math> of sequences <math>(x_n)_{n\in\mathbb{N}}</math> of complex numbers such that the series <math>\sum_{n\in\mathbb{N}}|x_n|^2</math> converges. If <math>x = (x_n)_{n\in\mathbb{N}}</math> and <math>y = (y_n)_{n\in\mathbb{N}}</math> are two vectors of <math>H</math> we denote by <math>\langle x,y\rangle</math> their scalar product: |
+ | == [[GoI for MELL: partial isometries|Partial isometries]] == |
| − | : <math>\langle x, y\rangle = \sum_{n\in\mathbb{N}} x_n\bar y_n</math>. |
||
| − | Two vectors of <math>H</math> are ''othogonal'' if their scalar product is nul. This notion is not to be confused with the orthogonality of operators defined above. The ''norm'' of a vector is the square root of the scalar product with itself: |
+ | The first step is to build the proof space. This is constructed as a special set of partial isometries on a separable Hilbert space <math>H</math> which turns out to be generated by partial permutations on the canonical basis of <math>H</math>. |
| − | : <math>\|x\| = \sqrt{\langle x, x\rangle}</math>. |
||
| − | Let us denote by <math>(e_k)_{k\in\mathbb{N}}</math> the canonical hilbertian basis of <math>H</math>: <math>e_k = (\delta_{kn})_{n\in\mathbb{N}}</math> where <math>\delta_{kn}</math> is the Kroenecker symbol. Thus if <math>x=(x_n)_{n\in\mathbb{N}}</math> is a sequence in <math>H</math> we have: |
+ | These so-called ''<math>p</math>-isometries'' enjoy some nice properties, the most important one being that a <math>p</math>-isometry is a sum of <math>p</math>-isometries iff all the terms of the sum have disjoint domains and disjoint codomains. As a consequence we get that a sum of <math>p</math>-isometries is null iff each term of the sum is null. |
| − | : <math> x = \sum_{n\in\mathbb{N}} x_ne_n</math>. |
||
| − | In this article we call ''operator'' on <math>H</math> a ''continuous'' linear map from <math>H</math> to <math>H</math>. Continuity is equivalent to the fact that operators are ''bounded'', which means that one may define the ''norm'' of an operator <math>u</math> as the sup on the unit ball of the norms of its values: |
+ | A second important property is that operators on <math>H</math> can be ''externalized'' using <math>p</math>-isometries into operators acting on <math>H\oplus H</math>, and conversely operators on <math>H\oplus H</math> may be ''internalized'' into operators on <math>H</math>. This is widely used in the sequel. |
| − | : <math>\|u\| = \sup_{\{x\in H,\, \|x\| = 1\}}\|u(x)\|</math>. |
||
| − | The set of (bounded) operators is denoted <math>\mathcal{B}(H)</math>. This is our proof space. |
+ | == [[GoI for MELL: the *-autonomous structure|The *-autonomous structure]] == |
| − | The ''range'' or ''codomain'' of the operator <math>u</math> is the set of images of vectors; the ''kernel'' of <math>u</math> is the set of vectors that are anihilated by <math>u</math>; the ''domain'' of <math>u</math> is the set of vectors orthogonal to the kernel: |
+ | The second step is to interpret the linear logic multiplicative operations, most importantly the cut rule. |
| − | : <math>\mathrm{Codom}(u) = \{u(x),\, x\in H\}</math>; |
+ | Internalization/externalization is the key for this: typically the type <math>A\tens B</math> is interpreted by a set of <math>p</math>-isometries which are internalizations of operators acting on <math>H\oplus H</math>. |
| − | : <math>\mathrm{Ker}(u) = \{x\in H,\, u(x) = 0\}</math>; |
||
| − | : <math>\mathrm{Dom}(u) = \mathrm{Ker}(u)\orth = \{x\in H,\, \forall y\in\mathrm{Ker}(u), \langle x, y\rangle = 0\}</math>. |
||
| − | These three sets are closed subspaces of <math>H</math>. |
+ | The (interpretation of) the cut-rule is defined in two steps: firstly we use nilpotency to define an operation corresponding to lambda-calculus application which given two <math>p</math>-isometries in respectively <math>A\limp B</math> and <math>A</math> produces an operator in <math>B</math>. From this we deduce the composition and finally obtain a structure of *-autonomous category, that is a model of multiplicative linear logic. |
| − | The ''adjoint'' of an operator <math>u</math> is the operator <math>u^*</math> defined by <math>\langle u(x), y\rangle = \langle x, u^*(y)\rangle</math> for any <math>x,y\in H</math>. |
+ | == [[GoI for MELL: exponentials|The exponentials]] == |
| − | A ''projector'' is an idempotent operator of norm <math>1</math>, that is an operator <math>p</math> such that <math>p^2 = p</math> and <math>\|p\| = 1</math>. A projector is auto-adjoint and its domain is equal to its codomain. |
+ | Finally we turn to define exponentials, that is connectives managing duplication. To do this we introduce an isomorphism (induced by a <math>p</math>-isometry) between <math>H</math> and <math>H\tens H</math>: the first component of the tensor is intended to hold the address of the the copy whereas the second component contains the content of the copy. |
| − | A ''partial isometry'' is an operator <math>u</math> satisfying <math>uu^* u = u</math>; as a consequence <math>uu^*</math> is a projector the range of which is the range of <math>u</math>. Similarly <math>u^* u</math> is also a projector the range of which is the domain of <math>u</math>. The restriction of <math>u</math> to its domain is an isometry. Projectors are particular examples of partial isometries. |
+ | We eventually get a quasi-model of full MELL; quasi in the sense that if we can construct <math>p</math>-isometries for usual structural operations in MELL (contraction, dereliction, digging), the interpretation of linear logic proofs is not invariant w.r.t. cut elimination in general. It is however invariant in some good cases, which are enough to get a correction theorem for the interpretation. |
| − | If <math>u</math> is a partial isometry then <math>u^*</math> is also a partial isometry the domain of which is the codomain of <math>u</math> and the codomain of which is the domain of <math>u</math>. |
+ | = The Geometry of Interaction as an abstract machine = |
| − | If the domain of <math>u</math> is <math>H</math> that is if <math>u^* u = 1</math> we say that <math>u</math> has ''full domain'', and similarly for codomain. If <math>u</math> and <math>v</math> are two partial isometries, the equation <math>uu^* + vv^* = 1</math> means that the codomains of <math>u</math> and <math>v</math> are orthogonal and that their direct sum is <math>H</math>. |
+ | = Notes and references = |
| − | === Partial permutations and partial isometries === |
+ | <references/> |
| − | |||
| − | It turns out that most of the operators needed to interpret logical operations are generated by ''partial permutations'' on the basis, which in particular entails that they are partial isometries. |
||
| − | |||
| − | More precisely a partial permutation <math>\varphi</math> on <math>\mathbb{N}</math> is a function defined on a subset <math>D_\varphi</math> of <math>\mathbb{N}</math> which is one-to-one onto a subset <math>C_\varphi</math> of <math>\mathbb{N}</math>. <math>D_\varphi</math> is called the ''domain'' of <math>\varphi</math> and <math>C_\varphi</math> its ''codomain''. Partial permutations may be composed: if <math>\psi</math> is another partial permutation on <math>\mathbb{N}</math> then <math>\varphi\circ\psi</math> is defined by: |
||
| − | |||
| − | : <math>n\in D_{\varphi\circ\psi}</math> iff <math>n\in D_\psi</math> and <math>\psi(n)\in D_\varphi</math>; |
||
| − | : if <math>n\in D_{\varphi\circ\psi}</math> then <math>\varphi\circ\psi(n) = \varphi(\psi(n))</math>; |
||
| − | : the codomain of <math>\varphi\circ\psi</math> is the image of the domain. |
||
| − | |||
| − | Partial permutations are well known to form a structure of ''inverse monoid'' that we detail now. |
||
| − | |||
| − | A ''partial identitie'' is a partial permutation <math>1_D</math> whose domain and codomain are both equal to a subset <math>D</math> on which <math>1_D</math> is the identity function. Among partial identities one finds the identity on the empty subset, that is the empty map, that we will denote as <math>0</math> and the identity on <math>\mathbb{N}</math> that we will denote by <math>1</math>. This latter permutation is the neutral for composition. |
||
| − | |||
| − | If <math>\varphi</math> is a partial permutation there is an inverse partial permutation <math>\varphi^{-1}</math> whose domain is <math>D_{\varphi^{-1}} = C_{\varphi}</math> and who satisfies: |
||
| − | |||
| − | : <math>\varphi^{-1}\circ\varphi = 1_{D_\varphi}</math> |
||
| − | : <math>\varphi\circ\varphi^{-1} = 1_{C_\varphi}</math> |
||
| − | |||
| − | Given a partial permutation <math>\varphi</math> one defines a partial isometry <math>u_\varphi</math> by: |
||
| − | : <math>u_\varphi(e_n) = |
||
| − | \begin{cases} |
||
| − | e_{\varphi(n)} & \text{ if }n\in D_\varphi,\\ |
||
| − | 0 & \text{ otherwise.} |
||
| − | \end{cases} |
||
| − | </math> |
||
| − | In other terms if <math>x=(x_n)_{n\in\mathbb{N}}</math> is a sequence in <math>\ell^2</math> then <math>u_\varphi(x)</math> is the sequence <math>(y_n)_{n\in\mathbb{N}}</math> defined by: |
||
| − | : <math>y_n = x_{\varphi^{-1}(n)}</math> if <math>n\in C_\varphi</math>, <math>0</math> otherwise. |
||
| − | |||
| − | The domain of <math>u_\varphi</math> is the subspace spaned by the family <math>(e_n)_{n\in D_\varphi}</math> and the codomain of <math>u_\varphi</math> is the subspace spaned by <math>(e_n)_{n\in C_\varphi}</math>. As a particular case if <math>\varphi</math> is <math>1_D</math> the partial identity on <math>D</math> then <math>u_\varphi</math> is the projector on the subspace spaned by <math>(e_n)_{n\in D}</math>. |
||
| − | |||
| − | If <math>\psi</math> is another partial permutation then we have: |
||
| − | : <math>u_\varphi u_\psi = u_{\varphi\circ\psi}</math>. |
||
| − | |||
| − | If <math>\varphi</math> is a partial permutation then the adjoint of <math>u_\varphi</math> is: |
||
| − | : <math>u_\varphi^* = u_{\varphi^{-1}}</math>. |
||
| − | |||
| − | In particular the projector on the domain of <math>u_{\varphi}</math> is given by: |
||
| − | : <math>u^*_\varphi u_\varphi = u_{1_{D_\varphi}}</math>. |
||
| − | |||
| − | and similarly the projector on the codomain of <math>u_\varphi</math> is: |
||
| − | : <math>u_\varphi u_\varphi^* = u_{1_{C_\varphi}}</math>. |
||
| − | |||
| − | == Interpreting the multiplicative connectives == |
||
| − | |||
| − | Recall that when <math>u</math> and <math>v</math> are operators we denote by <math>u\perp v</math> the fact that <math>uv</math> is nilpotent, and that <math>\bot</math> denotes the set of nilpotent operators so that <math>u\perp v</math> iff <math>uv\in\bot</math>. |
||
| − | |||
| − | If <math>X</math> is set of operators also recall that <math>X\orth</math> denotes the set of dual operators: |
||
| − | : <math>X\orth = \{v\in \mathcal{B}(H) \text{ such that }\forall u\in X, uv \in\bot\}</math>. |
||
| − | |||
| − | There are a few properties of this duality that we will use without mention in the sequel; let <math>X</math> and <math>Y</math> be sets of operators: |
||
| − | : <math>X\subset X\biorth</math>; |
||
| − | : <math>X\orth = X\triorth</math>. |
||
| − | : if <math>X\subset Y</math> then <math>Y\orth\subset X\orth</math>; |
||
| − | |||
| − | In particular <math>X\orth</math> is always a type (equal to its biorthogonal). We say that <math>X</math> ''generates'' the type <math>X\biorth</math>. |
||
| − | |||
| − | === The tensor and the linear application === |
||
| − | |||
| − | Our first step is, given two types <math>A</math> and <math>B</math>, to construct the type <math>A\tens B</math>. For this purpose we define an isomorphism <math>H\oplus H \cong H</math> by <math>x\oplus y\rightsquigarrow p(x)+q(y)</math> where <math>p:H\mapsto H</math> and <math>q:H\mapsto H</math> are partial isometries given by: |
||
| − | |||
| − | : <math>p(e_n) = e_{2n}</math>, |
||
| − | : <math>q(e_n) = e_{2n+1}</math>. |
||
| − | |||
| − | From the definition <math>p</math> and <math>q</math> have full domain, that is satisfy <math>p^* p = q^* q = 1</math>. On the other hand their codomains are orthogonal, thus we have <math>p^* q = q^* p = 0</math>. We also have <math>pp^* + qq^* = 1</math> although this property is not needed in the sequel. |
||
| − | |||
| − | Note that the choice of <math>p</math> and <math>q</math> is actually arbitrary, any two partial isometries with full domain and orthogonal codomains would do the job. |
||
| − | |||
| − | Let <math>U</math> be an operator on <math>H\oplus H</math>. We can write <math>U</math> as a matrix: |
||
| − | : <math>U = \begin{pmatrix} |
||
| − | U_{11} & U_{12}\\ |
||
| − | U_{21} & U_{22} |
||
| − | \end{pmatrix}</math> |
||
| − | where each <math>U_{ij}</math> operates on <math>H</math>. |
||
| − | |||
| − | Now through the isomorphism <math>H\oplus H\cong H</math> we may transform <math>U</math> into the operator <math>u</math> on <math>H</math> defined by: |
||
| − | |||
| − | : <math>u = pU_{11}p^* + pU_{12}q^* + qU_{21}p^* + qU_{22}q^*</math>. |
||
| − | |||
| − | We call <math>u</math> the ''internalization'' of <math>U</math>. Conversely given an operator <math>u</math> on <math>H</math> we may externalize it obtaining an operator <math>U</math> on <math>H\oplus H</math>: |
||
| − | : <math>U_{11} = p^*up</math>; |
||
| − | : <math>U_{12} = p^*uq</math>; |
||
| − | : <math>U_{21} = q^*up</math>; |
||
| − | : <math>U_{22} = q^*uq</math>. |
||
| − | |||
| − | Given <math>A</math> and <math>B</math> two types, we define their tensor by: |
||
| − | |||
| − | : <math>A\tens B = \{pup^* + qvq^*, u\in A, v\in B\}\biorth</math> |
||
| − | |||
| − | Note the closure by biorthogonal to make sure that we obtain a type. From what precedes we see that <math>A\tens B</math> is generated by the internalizations of operators on <math>H\oplus H</math> of the form: |
||
| − | : <math>\begin{pmatrix} |
||
| − | u & 0\\ |
||
| − | 0 & v |
||
| − | \end{pmatrix}</math> |
||
| − | |||
| − | As with orthogonality we use here the notation <math>\tens</math> in a specific sense: the tensor of two types should not be confused with the tensor of vectors or the tensor of spaces. |
||
| − | |||
| − | The linear implication is derived from the tensor by duality: given two types <math>A</math> and <math>B</math> the type <math>A\limp B</math> is defined by: |
||
| − | : <math>A\limp B = (A\tens B\orth)\orth</math>. |
||
| − | |||
| − | Unfolding this definition we see that we have: |
||
| − | : <math>A\limp B = \{u\in\mathcal{B}(H)\text{ such that } \forall v\in A, \forall w\in B\orth,\, u(pvp^* + qwq^*) \in\bot\}</math>. |
||
| − | |||
| − | === The idendity === |
||
| − | |||
| − | As an example of the internalization/externalization procedure, let us give the example of the (interpretation of the) identity. Given a type <math>A</math> we are to find an operator <math>\iota</math> in type <math>A\limp A</math>, thus satisfying: |
||
| − | : <math>\forall u\in A, v\in A\orth,\, \iota(pup^* + qvq^*)\in\bot</math>. |
||
| − | |||
| − | An easy solution is to take <math>\iota = pq^* + qp^*</math>. In this way we get <math>\iota(pup^* + qvq^*) = qup^* + pvq^*</math>. Therefore <math>(\iota(pup^* + qvq^*))^2 = quvq^* + pvup^*</math>, from which one deduces that this operator is nilpotent iff <math>uv</math> is nilpotent. It is the case since <math>u</math> is in <math>A</math> and <math>v</math> in <math>A\orth</math>. |
||
| − | |||
| − | It is interesting to note that the <math>\iota</math> thus defined is actually the internalization of the operator on <math>H\oplus H</math> given by the matrix: |
||
| − | : <math>\begin{pmatrix}0 & 1\\1 & 0\end{pmatrix}</math>. |
||
| − | |||
| − | We will see once the composition is defined that the <math>\iota</math> operator is the interpretation of the identity proof, as expected. |
||
| − | |||
| − | = The Geometry of Interaction as an abstract machine = |
||
Latest revision as of 16:39, 30 September 2011
The geometry of interaction, GoI in short, was defined in the early nineties by Girard as an interpretation of linear logic into operators algebra: formulae were interpreted by Hilbert spaces and proofs by partial isometries.
This was a striking novelty as it was the first time that a mathematical model of logic (lambda-calculus) didn't interpret a proof of 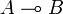 as a morphism from A to B and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on
as a morphism from A to B and proof composition (cut rule) as the composition of morphisms. Rather the proof was interpreted as an operator acting on 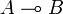 , that is a morphism from
, that is a morphism from 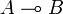 to
to  . For proof composition the problem was then, given an operator on
. For proof composition the problem was then, given an operator on 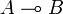 and another one on
and another one on 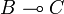 to construct a new operator on
to construct a new operator on 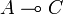 . This problem was solved by the execution formula that bares some formal analogies with Kleene's formula for recursive functions. For this reason GoI was claimed to be an operational semantics, as opposed to traditionnal denotational semantics.
. This problem was solved by the execution formula that bares some formal analogies with Kleene's formula for recursive functions. For this reason GoI was claimed to be an operational semantics, as opposed to traditionnal denotational semantics.
The first instance of the GoI was restricted to the MELL fragment of linear logic (Multiplicative and Exponential fragment) which is enough to encode lambda-calculus. Since then Girard proposed several improvements: firstly the extension to the additive connectives known as Geometry of Interaction 3 and more recently a complete reformulation using Von Neumann algebras that allows to deal with some aspects of implicit complexity
The GoI has been a source of inspiration for various authors. Danos and Regnier have reformulated the original model exhibiting its combinatorial nature using a theory of reduction of paths in proof-nets and showing the link with abstract machines; the execution formula appears as the composition of two automata interacting through a common interface. Also the execution formula has rapidly been understood as expressing the composition of strategies in game semantics. It has been used in the theory of sharing reduction for lambda-calculus in the Abadi-Gonthier-Lévy reformulation and simplification of Lamping's representation of sharing. Finally the original GoI for the MELL fragment has been reformulated in the framework of traced monoidal categories following an idea originally proposed by Joyal.
Contents |
[edit] The Geometry of Interaction as operators
The original construction of GoI by Girard follows a general pattern already mentionned in the section on coherent semantics under the name symmetric reducibility and that was first put to use in phase semantics. First set a general space P called the proof space because this is where the interpretations of proofs will live. Make sure that P is a (not necessarily commutative) monoid. In the case of GoI, the proof space is a subset of the space of bounded operators on 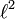 .
.
Second define a particular subset of P that will be denoted by 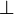 ; then derive a duality on P: for
; then derive a duality on P: for 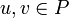 , u and v are dual[1]iff
, u and v are dual[1]iff 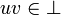 .
.
Such a duality defines an orthogonality relation, with the usual derived definitions and properties.
For the GoI, two dualities have proved to work; we will consider the first one: nilpotency, ie, 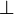 is the set of nilpotent operators in P. Let us explicit this: two operators u and v are dual if there is a nonnegative integer n such that (uv)n = 0. This duality is symmetric: if uv is nilpotent then vu is nilpotent also.
is the set of nilpotent operators in P. Let us explicit this: two operators u and v are dual if there is a nonnegative integer n such that (uv)n = 0. This duality is symmetric: if uv is nilpotent then vu is nilpotent also.
Last define a type as a subset T of the proof space that is equal to its bidual: 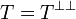 . This means that
. This means that 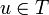 iff for all operator
iff for all operator 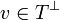 , that is such that
, that is such that 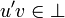 for all
for all 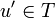 , we have
, we have 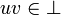 .
.
The real work[2]is now to interpret logical operations, that is to associate a type to each formula, an object to each proof and show the adequacy lemma: if u is the interpretation of a proof of the formula A then u belongs to the type associated to A.
[edit] Partial isometries
The first step is to build the proof space. This is constructed as a special set of partial isometries on a separable Hilbert space H which turns out to be generated by partial permutations on the canonical basis of H.
These so-called p-isometries enjoy some nice properties, the most important one being that a p-isometry is a sum of p-isometries iff all the terms of the sum have disjoint domains and disjoint codomains. As a consequence we get that a sum of p-isometries is null iff each term of the sum is null.
A second important property is that operators on H can be externalized using p-isometries into operators acting on 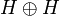 , and conversely operators on
, and conversely operators on 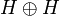 may be internalized into operators on H. This is widely used in the sequel.
may be internalized into operators on H. This is widely used in the sequel.
[edit] The *-autonomous structure
The second step is to interpret the linear logic multiplicative operations, most importantly the cut rule.
Internalization/externalization is the key for this: typically the type 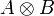 is interpreted by a set of p-isometries which are internalizations of operators acting on
is interpreted by a set of p-isometries which are internalizations of operators acting on 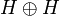 .
.
The (interpretation of) the cut-rule is defined in two steps: firstly we use nilpotency to define an operation corresponding to lambda-calculus application which given two p-isometries in respectively 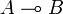 and A produces an operator in B. From this we deduce the composition and finally obtain a structure of *-autonomous category, that is a model of multiplicative linear logic.
and A produces an operator in B. From this we deduce the composition and finally obtain a structure of *-autonomous category, that is a model of multiplicative linear logic.
[edit] The exponentials
Finally we turn to define exponentials, that is connectives managing duplication. To do this we introduce an isomorphism (induced by a p-isometry) between H and 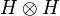 : the first component of the tensor is intended to hold the address of the the copy whereas the second component contains the content of the copy.
: the first component of the tensor is intended to hold the address of the the copy whereas the second component contains the content of the copy.
We eventually get a quasi-model of full MELL; quasi in the sense that if we can construct p-isometries for usual structural operations in MELL (contraction, dereliction, digging), the interpretation of linear logic proofs is not invariant w.r.t. cut elimination in general. It is however invariant in some good cases, which are enough to get a correction theorem for the interpretation.
[edit] The Geometry of Interaction as an abstract machine
[edit] Notes and references
- ↑ In modern terms one says that u and v are polar.
- ↑ The difficulty is to find the right duality that will make logical operations interpretable. General conditions that allows to achieve this have been formulated by Hyland and Schalk thanks to their theory of double glueing.