Fragment
(Removing all content from page) |
|||
| Line 1: | Line 1: | ||
| + | In general, a '''fragment''' of a logical system ''S'' is a logical system obtained by restricting the language of ''S'', and by restricting the rules of ''S'' accordingly. In linear logic, the most well known fragments are obtained by combining/removing in different ways the classes of connectives present in the [[Sequent calculus|language of linear logic]] itself: |
||
| + | |||
| + | * '''Multiplicative connectives:''' the conjunction <math>\tens</math> (''tensor'') and the disjunction <math>\parr</math> (''par''), with their respective units <math>\one</math> (''one'') and <math>\bot</math> (''bottom''); these connectives are the combinatorial base of linear logic (permutations, circuits, etc.). |
||
| + | * '''Additive connectives:''' the conjunction <math>\with</math> (''with'') and the disjunction <math>\plus</math> (''plus''), with their respective units <math>\top</math> (''top'') and <math>\zero</math> (''zero''); the computational content of these connectives, which behave more closely to their intuitionistic counterparts (e.g., <math>A\with B\limp A</math> and <math>A\with B\limp B</math> are provable), is strongly related to choice (''if...then...else'', product and sum types, etc.). |
||
| + | * '''Exponential connectives:''' the modalities <math>\oc</math> (''of course'') and <math>\wn</math> (''why not'') handle the structural rules in linear logic, and are necessary to recover the expressive power of intuitionistic or classical logic. |
||
| + | * '''Quantifiers:''' just as in classical logic, quantifiers may be added to propositional linear logic, at any order. The most frequently considered are the second order ones (in analogy with System F). |
||
| + | |||
| + | The additive and exponential connectives, if taken alone, yield fragments of limited interest, so one usually considers only fragments containing at least the multiplicative connectives (perhaps without units). It is important to observe that the [[Sequent calculus#Properties of proofs|cut-elimination rules]] of linear logic do not introduce connectives belonging to a different class than that of the pair of dual formulas whose cut is being reduced. Hence, any fragment defined by combining the above classes will enjoy cut-elimination. |
||
| + | |||
| + | Conventionally, if <math>LL</math> denotes full linear logic, its fragments are denoted by prefixing <math>LL</math> with letters corresponding to the classes of connectives being considered: <math>M</math> for multiplicative connectives, <math>A</math> for additive connectives, and <math>E</math> for exponential connectives. Additional subscripts may specify whether units and/or quantifiers are present or not, and, for quantifiers, at what order (see the article on [[notations]]). |
||
| + | |||
| + | == Motivations == |
||
| + | |||
| + | The main interest of studying fragments of linear logic is that these are usually simpler than the whole system, so that certain properties may be first analyzed on fragments, and then extended or adapted to increasingly larger fragments. It may also be interesting to see, given a property that does not hold for full linear logic, whether it holds for a fragment, and where the "breaking point" is situated. Examples of such questions include: |
||
| + | |||
| + | * '''logical complexity:''' proving cut-elimination for full linear logic with second order quantification is equivalent to proving the consistency of second order Peano arithmetic (Girard, via [[Translations of intuitionistic logic|translations of System F]] in linear logic). One may expect that smaller fragments have lower logical complexity. |
||
| + | * '''provability:''' the ''provability problem'' for a logical system ''S'' is defined as follows: given a formula <math>A</math> in the language of ''S'', is <math>A</math> provable in ''S''? This problem is undecidable in full linear logic with first order quantifiers (again, because [[Translations of classical logic|classical logic can be translated]] in linear logic). On what fragments does it become decidable? And if it does, what is its computational complexity? |
||
| + | * '''computational complexity of cut-elimination:''' the ''cut-elimination problem'' (Mairson-Terui) for a logical system ''S'' is defined as follows: given two proofs of <math>A</math> in ''S'', do they reduce to the same cut-free proof? Although decidable (thanks to strong normalization), this problem is not elementary recursive in full linear logic with first order quantification (Statman, again via the above-mentioned translations). Does the problem fall into any interesting complexity class when applied to fragments? |
||
| + | * '''proof nets:''' the definition of proof nets, and in particular the formulation of correctness criteria and the study of their complexity, is a good example of how a methodology can be applied to a small fragment of linear logic and later adapted (more or less successfully) to wider fragments. |
||
| + | |||
| + | == Multiplicative linear logic == |
||
| + | |||
| + | Multiplicative linear logic (<math>MLL</math>) is the simplest of the well known fragments of linear logic. Its formulas are obtained by combining propositional atoms with the connectives ''tensor'' and ''par'' only. As a consequence, the [[Sequent calculus#Sequents and proofs|sequent calculus]] of <math>MLL</math> is limited to the rules <math>\rulename{axiom}</math>, <math>\rulename{cut}</math>, <math>\tens</math>, and <math>\parr</math>. These rules actually determine the multiplicative connectives: if a dual pair of connectives <math>\tens'</math> and <math>\parr'</math> is introduced, with the same rules as <math>\tens</math> and <math>\parr</math>, respectively, then one can show <math>A\tens' B</math> to be provably equivalent to <math>A\tens B</math> (and, dually, <math>A\parr'B</math> to be provably equivalent to <math>A\parr B</math>). |
||
| + | |||
| + | The cut-elimination problem for <math>MLL</math> is <math>\mathbf P</math>-complete (Mairson-Terui), even though there exists a deterministic algorithm solving the problem in logarithmic space if one considers only [[Sequent calculus#Properties of proofs|eta-expanded]] proofs (Mairson-Terui). On the other hand, provability for <math>MLL</math> is <math>\mathbf{NP}</math>-complete. |
||
| + | |||
| + | Another multiplicative fragment, less considered in the literarure, can be defined by using the units <math>\one</math> and <math>\bot</math> instead of the propositional atoms. In this fragment, denoted by <math>MLL_u</math>, one can also eliminate the <math>\rulename{axiom}</math> rule from sequent calculus, since it is redundant. <math>MLL_u</math> is even simpler than <math>MLL</math>: its provability problem is in <math>\mathbf P</math>, and, since all proofs are eta-expandend, its cut-elimination problem is in <math>\mathbf L</math>. |
||
| + | |||
| + | The union of <math>MLL</math> and <math>MLL_u</math> is the full propositional multiplicative fragment of linear logic, and is denoted by <math>MLL_0</math>. It has the same properties as <math>MLL</math>, which shows that the presence/absence of propositional atoms (and of the <math>\rulename{axiom}</math> rule) has a non-trivial effect on the complexity of provability and cut-elimination, i.e., the complexity is not altered iff <math>\mathbf P\subsetneq\mathbf{NP}</math> and <math>\mathbf L\subsetneq\mathbf P</math>, respectively. |
||
| + | |||
| + | If we add second order quantifiers to <math>MLL</math> (resp. <math>MLL_u</math>), we obtain a system denoted by <math>MLL_2</math> (resp. <math>MLL_{02}</math>). In <math>MLL_{02}</math> one can show that <math>\one</math> and <math>\bot</math> are provably equivalent to <math>\forall X.(X\orth\parr X)</math> and <math>\exists X.(X\orth\tens X)</math>, respectively. Hence, <math>MLL_2</math> is as expressive as <math>MLL_{02}</math>. |
||
| + | |||
| + | == Multiplicative additive linear logic == |
||
| + | |||
| + | == Multiplicative exponential linear logic == |
||
| + | |||
| + | == Quantifiers == |
||
| + | |||
| + | == Intuitionistic linear logic == |
||
| + | |||
| + | == The provability problem == |
||
| + | |||
| + | == The cut-elimination problem == |
||
Revision as of 20:29, 1 March 2009
In general, a fragment of a logical system S is a logical system obtained by restricting the language of S, and by restricting the rules of S accordingly. In linear logic, the most well known fragments are obtained by combining/removing in different ways the classes of connectives present in the language of linear logic itself:
- Multiplicative connectives: the conjunction
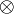(tensor) and the disjunction 
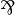(par), with their respective units 
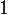(one) and 
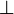(bottom); these connectives are the combinatorial base of linear logic (permutations, circuits, etc.).
- Additive connectives: the conjunction
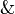(with) and the disjunction 
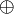(plus), with their respective units 
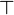(top) and 
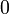(zero); the computational content of these connectives, which behave more closely to their intuitionistic counterparts (e.g., 
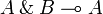and 
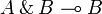are provable), is strongly related to choice (if...then...else, product and sum types, etc.).
- Exponential connectives: the modalities
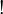(of course) and 
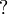(why not) handle the structural rules in linear logic, and are necessary to recover the expressive power of intuitionistic or classical logic.
- Quantifiers: just as in classical logic, quantifiers may be added to propositional linear logic, at any order. The most frequently considered are the second order ones (in analogy with System F).
The additive and exponential connectives, if taken alone, yield fragments of limited interest, so one usually considers only fragments containing at least the multiplicative connectives (perhaps without units). It is important to observe that the cut-elimination rules of linear logic do not introduce connectives belonging to a different class than that of the pair of dual formulas whose cut is being reduced. Hence, any fragment defined by combining the above classes will enjoy cut-elimination.
Conventionally, if LL denotes full linear logic, its fragments are denoted by prefixing LL with letters corresponding to the classes of connectives being considered: M for multiplicative connectives, A for additive connectives, and E for exponential connectives. Additional subscripts may specify whether units and/or quantifiers are present or not, and, for quantifiers, at what order (see the article on notations).
Contents |
Motivations
The main interest of studying fragments of linear logic is that these are usually simpler than the whole system, so that certain properties may be first analyzed on fragments, and then extended or adapted to increasingly larger fragments. It may also be interesting to see, given a property that does not hold for full linear logic, whether it holds for a fragment, and where the "breaking point" is situated. Examples of such questions include:
- logical complexity: proving cut-elimination for full linear logic with second order quantification is equivalent to proving the consistency of second order Peano arithmetic (Girard, via translations of System F in linear logic). One may expect that smaller fragments have lower logical complexity.
- provability: the provability problem for a logical system S is defined as follows: given a formula A in the language of S, is A provable in S? This problem is undecidable in full linear logic with first order quantifiers (again, because classical logic can be translated in linear logic). On what fragments does it become decidable? And if it does, what is its computational complexity?
- computational complexity of cut-elimination: the cut-elimination problem (Mairson-Terui) for a logical system S is defined as follows: given two proofs of A in S, do they reduce to the same cut-free proof? Although decidable (thanks to strong normalization), this problem is not elementary recursive in full linear logic with first order quantification (Statman, again via the above-mentioned translations). Does the problem fall into any interesting complexity class when applied to fragments?
- proof nets: the definition of proof nets, and in particular the formulation of correctness criteria and the study of their complexity, is a good example of how a methodology can be applied to a small fragment of linear logic and later adapted (more or less successfully) to wider fragments.
Multiplicative linear logic
Multiplicative linear logic (MLL) is the simplest of the well known fragments of linear logic. Its formulas are obtained by combining propositional atoms with the connectives tensor and par only. As a consequence, the sequent calculus of MLL is limited to the rules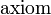 
, 
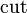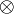, , and 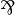. These rules actually determine the multiplicative connectives: if a dual pair of connectives 
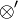and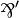 
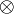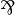is introduced, with the same rules as and , respectively, then one can show 
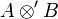to be provably equivalent to 
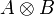(and, dually, 
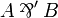to be provably equivalent to 
).
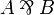The cut-elimination problem for MLL is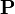 
-complete (Mairson-Terui), even though there exists a deterministic algorithm solving the problem in logarithmic space if one considers only eta-expanded proofs (Mairson-Terui). On the other hand, provability for MLL is 
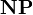-complete.
Another multiplicative fragment, less considered in the literarure, can be defined by using the units 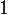and 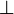instead of the propositional atoms. In this fragment, denoted by MLLu, one can also eliminate the 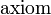rule from sequent calculus, since it is redundant. MLLu is even simpler than MLL: its provability problem is in 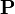, and, since all proofs are eta-expandend, its cut-elimination problem is in 
.
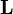The union of MLL and MLLu is the full propositional multiplicative fragment of linear logic, and is denoted by MLL0. It has the same properties as MLL, which shows that the presence/absence of propositional atoms (and of the 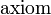rule) has a non-trivial effect on the complexity of provability and cut-elimination, i.e., the complexity is not altered iff 
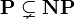and 
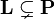, respectively.
If we add second order quantifiers to MLL (resp. MLLu), we obtain a system denoted by MLL2 (resp. MLL02). In MLL02 one can show that 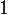and 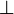are provably equivalent to 
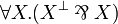and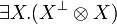 
, respectively. Hence, MLL2 is as expressive as MLL02.
