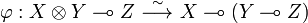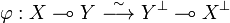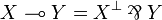Coherent semantics
Coherent semantics was invented by Girard in the paper The system F, 15 years later[1]with the objective of building a denotationnal interpretation of second order intuitionnistic logic (aka polymorphic lambda-calculus).
Coherent semantics is based on the notion of stable functions that was initially proposed by Gérard Berry. Stability is a condition on Scott continuous functions that expresses the determinism of the relation between the output and the input: the typical Scott continuous but non stable function is the parallel or because when the two inputs are both set to true, only one of them is the reason why the result is true but there is no way to determine which one.
A further achievement of coherent semantics was that it allowed to endow the set of stable functions from X to Y with a structure of domain, thus closing the category of coherent spaces and stable functions. However the most interesting point was the discovery of a special class of stable functions, linear functions, which was the first step leading to Linear Logic.
Contents |
The cartesian closed structure of coherent semantics
There are three equivalent definitions of coherent spaces: the first one, coherent spaces as domains, is interesting from a historical point of view as it emphazises the fact that coherent spaces are particular cases of Scott domains. The second one, coherent spaces as graphs, is the most commonly used and will be our "official" definition in the sequel. The last one, cliqued spaces is a particular example of a more general scheme that one could call "symmetric reducibility"; this scheme is underlying lots of constructions in linear logic such as phase semantics or the proof of strong normalisation for proof-nets.
Coherent spaces
A coherent space X is a collection of subsets of a set 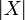 satisfying some conditions that will be detailed shortly. The elements of X are called the cliques of X (for reasons that will be made clear in a few lines). The set
satisfying some conditions that will be detailed shortly. The elements of X are called the cliques of X (for reasons that will be made clear in a few lines). The set 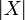 is called the web of X and its elements are called the points of X; thus a clique is a set of points. Note that the terminology is a bit ambiguous as the points of X are the elements of the web of X, not the elements of X.
is called the web of X and its elements are called the points of X; thus a clique is a set of points. Note that the terminology is a bit ambiguous as the points of X are the elements of the web of X, not the elements of X.
The definitions below give three equivalent conditions that have to be satisfied by the cliques of a coherent space.
As domains
The cliques of X have to satisfy:
- subset closure: if
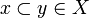 then
then 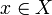 ,
,
- singletons:
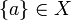 for
for 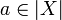 .
.
- binary compatibility: if A is a family of pairwise compatible cliques of X, that is if
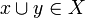 for any
for any 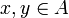 , then
, then 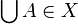 .
.
A coherent space is thus ordered by inclusion; one easily checks that it is a domain. In particular finite cliques of X correspond to compact elements.
As graphs
There is a reflexive and symetric relation 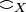 on
on 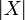 (the coherence relation) such that any subset x of
(the coherence relation) such that any subset x of 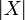 is a clique of X iff
is a clique of X iff 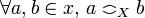 . In other terms X is the set of complete subgraphs of the simple unoriented graph of the
. In other terms X is the set of complete subgraphs of the simple unoriented graph of the 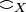 relation; this is the reason why elements of X are called cliques.
relation; this is the reason why elements of X are called cliques.
The strict coherence relation 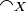 on X is defined by:
on X is defined by: 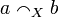 iff
iff 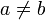 and
and 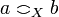 .
.
A coherent space in the domain sense is seen to be a coherent space in the graph sense by setting 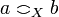 iff
iff 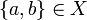 ; conversely one can check that cliques in the graph sense are subset closed and satisfy the binary compatibility condition.
; conversely one can check that cliques in the graph sense are subset closed and satisfy the binary compatibility condition.
A coherent space is completely determined by its web and its coherence relation, or equivalently by its web and its strict coherence.
As cliqued spaces
Definition (Duality)
Let 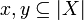 be two sets. We will say that they are dual, written
be two sets. We will say that they are dual, written 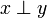 if their intersection contains at most one element:
if their intersection contains at most one element: 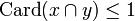 . As usual, it defines an orthogonality relation over
. As usual, it defines an orthogonality relation over 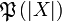 .
.
The last way to express the conditions on the cliques of a coherent space X is simply to say that we must have 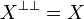 .
.
Equivalence of definitions
Let X be a cliqued space and define a relation on 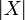 by setting
by setting 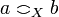 iff there is
iff there is 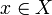 such that
such that 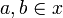 . This relation is obviously symetric; it is also reflexive because all singletons belong to X: if
. This relation is obviously symetric; it is also reflexive because all singletons belong to X: if 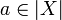 then {a} is dual to any element of
then {a} is dual to any element of 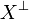 (actually {a} is dual to any subset of
(actually {a} is dual to any subset of 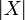 ), thus {a} is in
), thus {a} is in 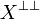 , thus in X.
, thus in X.
Let 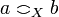 . Then
. Then 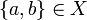 ; indeed there is an
; indeed there is an 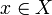 such that
such that 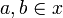 . This x is dual to any
. This x is dual to any 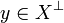 , that is meets any
, that is meets any 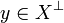 in a most one point. Since
in a most one point. Since 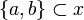 this is also true of {a,b}, so that {a,b} is in
this is also true of {a,b}, so that {a,b} is in 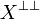 thus in X.
thus in X.
Now let x be a clique for 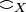 and y be an element of
and y be an element of 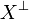 . Suppose
. Suppose 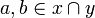 , then since a and b are coherent (by hypothesis on x) we have
, then since a and b are coherent (by hypothesis on x) we have 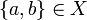 and since
and since 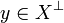 we must have that {a,b} and y meet in at most one point. Thus a = b and we have shown that x and y are dual. Since y was arbitrary this means that x is in
we must have that {a,b} and y meet in at most one point. Thus a = b and we have shown that x and y are dual. Since y was arbitrary this means that x is in 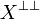 , thus in X. Finally we get that any set of pairwise coherent points of X is in X. Conversely given
, thus in X. Finally we get that any set of pairwise coherent points of X is in X. Conversely given 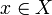 its points are obviously pairwise coherent so eventually we get that X is a coherent space in the graph sense.
its points are obviously pairwise coherent so eventually we get that X is a coherent space in the graph sense.
Conversely given a coherent space X in the graph sense, one can check that it is a cliqued space. Call anticlique a set 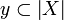 of pairwise incoherent points: for all a,b in y, if
of pairwise incoherent points: for all a,b in y, if 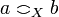 then a = b. Any anticlique intersects any clique in at most one point: let x be a clique and y be an anticlique, then if
then a = b. Any anticlique intersects any clique in at most one point: let x be a clique and y be an anticlique, then if 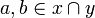 , since
, since 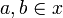 we have
we have 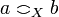 and since y is an anticlique we have a = b. Thus
and since y is an anticlique we have a = b. Thus 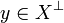 . Conversely given any
. Conversely given any 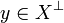 and
and 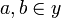 , suppose
, suppose 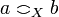 . Then
. Then 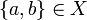 , thus
, thus 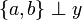 which entails that {a,b} has at most one point so that a = b: we have shown that any two elements of y are incoherent.
which entails that {a,b} has at most one point so that a = b: we have shown that any two elements of y are incoherent.
Thus the collection of anticliques of X is the dual 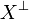 of X. Note that the incoherence relation defined above is reflexive and symetric, so that
of X. Note that the incoherence relation defined above is reflexive and symetric, so that 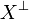 is a coherent space in the graph sense. Thus we can do for
is a coherent space in the graph sense. Thus we can do for 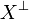 exactly what we've just done for X and consider the anti-anticliques, that is the anticliques for the incoherent relation which are the cliques for the in-incoherent relation. It is not difficult to see that this in-incoherence relation is just the coherence relation we started with; we thus obtain that
exactly what we've just done for X and consider the anti-anticliques, that is the anticliques for the incoherent relation which are the cliques for the in-incoherent relation. It is not difficult to see that this in-incoherence relation is just the coherence relation we started with; we thus obtain that 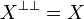 , so that X is a cliqued space.
, so that X is a cliqued space.
Stable functions
Definition (Stable function)
Let X and Y be two coherent spaces. A function 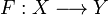 is stable if it satisfies:
is stable if it satisfies:
- it is non decreasing: for any
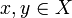 if
if 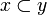 then
then 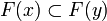 ;
;
- it is continuous (in the Scott sense): if A is a directed family of cliques of X, that is if for any
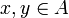 there is a
there is a 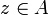 such that
such that 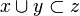 , then
, then 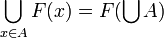 ;
;
- it satisfies the stability condition: if
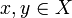 are compatible, that is if
are compatible, that is if 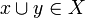 , then
, then 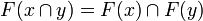 .
.
This definition is admitedly not very tractable. An equivalent and most useful caracterisation of stable functions is given by the following theorem.
Theorem
Let 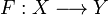 be a non-decreasing function from the coherent space X to the coherent space Y. The function F is stable iff it satisfies: for any
be a non-decreasing function from the coherent space X to the coherent space Y. The function F is stable iff it satisfies: for any 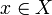 ,
, 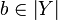 , if
, if 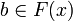 then there is a finite clique
then there is a finite clique 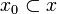 such that:
such that:
-
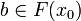 ,
,
- for any
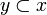 if
if 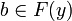 then
then 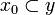 (x0 is the minimum sub-clique of x such that
(x0 is the minimum sub-clique of x such that 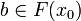 ).
).
Note that the stability condition doesn't depend on the coherent space structure and can be expressed more generally for continuous functions on domains. However, as mentionned in the introduction, the restriction to coherent spaces allows to endow the set of stable functions from X to Y with a structure of coherent space.
Definition (The space of stable functions)
Let X and Y be coherent spaces. We denote by Xfin the set of finite cliques of X. The function space 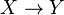 is defined by:
is defined by:
-
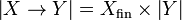 ,
,
-
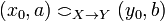 iff
iff 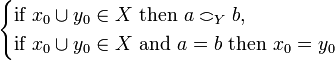 .
.
One could equivalently define the strict coherence relation on 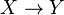 by:
by: 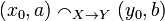 iff when
iff when 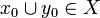 then
then 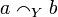 (equivalently
(equivalently 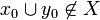 or
or 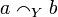 ).
).
Definition (Trace of a stable function)
Let 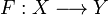 be a function. The trace of F is the set:
be a function. The trace of F is the set:
.
Theorem
F is stable iff Tr(F) is a clique of the function space 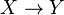
In particular the continuity of F entails that if x0 is minimal such that 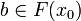 , then x0 is finite.
, then x0 is finite.
Definition (The evaluation function)
Let f be a clique in 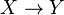 . We define a function
. We define a function 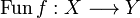 by:
by: 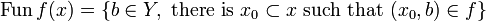 .
.
Theorem (Closure)
If f is a clique of the function space 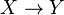 then we have
then we have 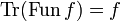 . Conversely if
. Conversely if 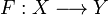 is a stable function then we have
is a stable function then we have 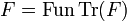 .
.
Cartesian product
Definition (Cartesian product)
Let X1 and X2 be two coherent spaces. We define the coherent space 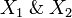 (read X1 with X2):
(read X1 with X2):
- the web is the disjoint union of the webs:
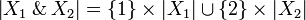 ;
;
- the coherence relation is the serie composition of the relations on X1 and X2:
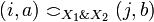 iff either
iff either  or i = j and
or i = j and  .
.
This definition is just the way to put a coherent space structure on the cartesian product. Indeed one easily shows the
Theorem
Given cliques x1 and x2 in X1 and X2, we define the subset 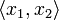 of
of 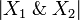 by:
by: 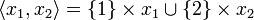 . Then
. Then 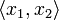 is a clique in
is a clique in 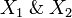 .
.
Conversely, given a clique 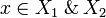 , for i = 1,2 we define
, for i = 1,2 we define 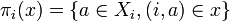 . Then πi(x) is a clique in Xi and the function
. Then πi(x) is a clique in Xi and the function 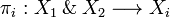 is stable.
is stable.
Furthemore these two operations are inverse of each other: 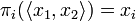 and
and 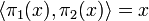 . In particular any clique in
. In particular any clique in 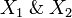 is of the form
is of the form 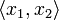 .
.
Altogether the results above (and a few other more that we shall leave to the reader) allow to get:
Theorem
The category of coherent spaces and stable functions is cartesian closed.
In particular this means that if we define 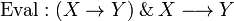 by:
by: 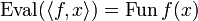 then Eval is stable.
then Eval is stable.
The monoidal structure of coherent semantics
Linear functions
Definition (Linear function)
A function 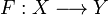 is linear if it is stable and furthemore satisfies: for any family A of pairwise compatible cliques of X, that is such that for any
is linear if it is stable and furthemore satisfies: for any family A of pairwise compatible cliques of X, that is such that for any 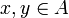 ,
, 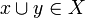 , we have
, we have 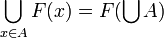 .
.
In particular if we take A to be the empty family, then we have 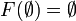 .
.
The condition for linearity is quite similar to the condition for Scott continuity, except that we dropped the constraint that A is directed. Linearity is therefore much stronger than stability: most stable functions are not linear.
However most of the functions seen so far are linear. Typically the function 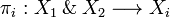 is linear from wich one may deduce that the with construction is also a cartesian product in the category of coherent spaces and linear functions.
is linear from wich one may deduce that the with construction is also a cartesian product in the category of coherent spaces and linear functions.
As with stable function we have an equivalent and much more tractable caracterisation of linear function:
Theorem
Let 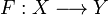 be a continuous function. Then F is linear iff it satisfies: for any clique
be a continuous function. Then F is linear iff it satisfies: for any clique 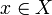 and any
and any 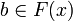 there is a unique
there is a unique 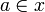 such that
such that 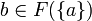 .
.
Just as the caracterisation theorem for stable functions allowed us to build the coherent space of stable functions, this theorem will help us to endow the set of linear maps with a structure of coherent space.
Definition (The linear functions space)
Let X and Y be coherent spaces. The linear function space 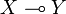 is defined by:
is defined by:
-
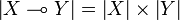 ,
,
-
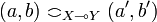 iff
iff 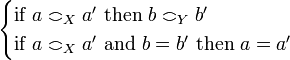
Equivalently one could define the strict coherence to be: 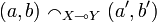 iff
iff 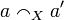 entails
entails 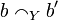 .
.
Definition (Linear trace)
Let 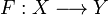 be a function. The linear trace of F denoted as LinTr(F) is the set:
be a function. The linear trace of F denoted as LinTr(F) is the set:
such that
.
Theorem
If F is linear then LinTr(F) is a clique of 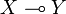 .
.
Definition (Evaluation of linear function)
Let f be a clique of 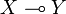 . We define the function
. We define the function 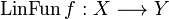 by:
by: 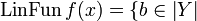 such that there is an
such that there is an 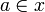 satisfying
satisfying 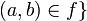 .
.
Theorem (Linear closure)
Let f be a clique in 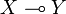 . Then we have
. Then we have 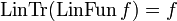 . Conversely if
. Conversely if 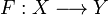 is linear then we have
is linear then we have 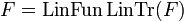 .
.
It remains to define a tensor product and we will get that the category of coherent spaces with linear functions is monoidal symetric (it is actually *-autonomous).
Tensor product
Definition (Tensor product)
Let X and Y be coherent spaces. Their tensor product 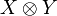 is defined by:
is defined by: 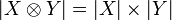 and
and 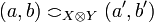 iff
iff 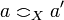 and
and 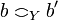 .
.
Theorem
The category of coherent spaces with linear maps and tensor product is monoidal symetric closed.
The closedness is a consequence of the existence of the linear isomorphism:
that is defined by its linear trace: 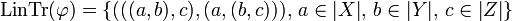 .
.
Linear negation
Definition (Linear negation)
Let X be a coherent space. We define the incoherence relation on 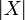 by:
by: 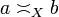 iff
iff 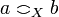 entails a = b. The incoherence relation is reflexive and symetric; we call dual or linear negation of X the associated coherent space denoted
entails a = b. The incoherence relation is reflexive and symetric; we call dual or linear negation of X the associated coherent space denoted 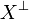 , thus defined by:
, thus defined by: 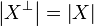 and
and 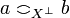 iff
iff 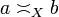 .
.
The cliques of 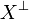 are called the anticliques of X. As seen in the section on cliqued spaces we have
are called the anticliques of X. As seen in the section on cliqued spaces we have 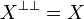 .
.
Theorem
The category of coherent spaces with linear maps, tensor product and linear negation is *-autonomous.
This is in particular consequence of the existence of the isomorphism:
defined by its linear trace: 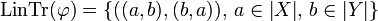 .
.
Exponentials
In linear algebra, bilinear maps may be factorized through the tensor product. Similarly there is a coherent space 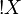 that allows to factorize stable functions through linear functions.
that allows to factorize stable functions through linear functions.
Definition (Of course)
Let X be a coherent space; recall that Xfin denotes the set of finite cliques of X. We define the space 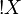 (read of course X) by:
(read of course X) by: 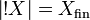 and
and 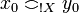 iff
iff 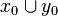 is a clique of X.
is a clique of X.
Thus a clique of 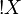 is a set of finite cliques of X the union of wich is a clique of X.
is a set of finite cliques of X the union of wich is a clique of X.
Theorem
Let X be a coherent space. Denote by 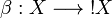 the stable function whose trace is:
the stable function whose trace is: 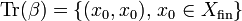 . Then for any coherent space Y and any stable function
. Then for any coherent space Y and any stable function 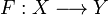 there is a unique linear function
there is a unique linear function 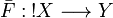 such that
such that 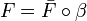 .
.
Furthermore we have 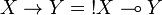 .
.
Theorem (The exponential isomorphism)
Let X and Y be two coherent spaces. Then there is a linear isomorphism:
.
The iso 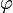 is defined by its trace:
is defined by its trace: 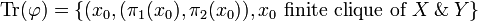 .
.
This isomorphism, that sends an additive structure (the web of a with is obtained by disjoint union) onto a multiplicative one (the web of a tensor is obtained by cartesian product) is the reason why the of course is called an exponential.
Dual connectives and neutrals
By linear negation all the constructions defined so far ( ) have a dual.
) have a dual.
The direct sum
The dual of  is
is  defined by:
defined by: 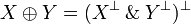 . An equivalent definition is given by:
. An equivalent definition is given by: 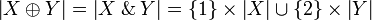 and
and 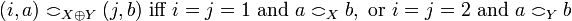 .
.
Theorem
Let x' be a clique of 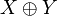 ; then x' is of the form
; then x' is of the form 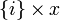 where
where 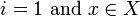 , or
, or 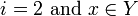 .
.
Denote  the function defined by
the function defined by 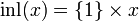 and by
and by  the function defined by
the function defined by 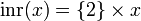 . Then inl and inr are linear.
. Then inl and inr are linear.
If 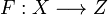 and
and 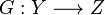 are linear functions then the function
are linear functions then the function 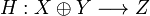 defined by H(inl(x)) = F(x) and H(inr(y)) = G(y) is linear.
defined by H(inl(x)) = F(x) and H(inr(y)) = G(y) is linear.
In other terms 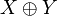 is the direct sum of X and Y. Note that in the theorem all functions are linear. Things doesn't work so smoothly for stable functions. Historically it was after noting this defect of coherent semantics w.r.t. the intuitionnistic implication that Girard was leaded to discover linear functions.
is the direct sum of X and Y. Note that in the theorem all functions are linear. Things doesn't work so smoothly for stable functions. Historically it was after noting this defect of coherent semantics w.r.t. the intuitionnistic implication that Girard was leaded to discover linear functions.
The par and the why not
We now come to the most mysterious constructions of coherent semantics: the duals of the tensor and the of course.
The par is the dual of the tensor, thus defined by: 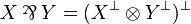 . From this one can deduce the definition in graph terms:
. From this one can deduce the definition in graph terms: 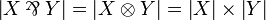 and
and 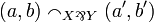 iff
iff 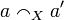 or
or 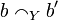 . With this definition one sees that we have:
. With this definition one sees that we have:
for any coherent spaces X and Y. This equation can be seen as an alternative definition of the par: 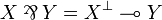 .
.
Similarly the dual of the of course is called why not defined by: 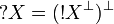 . From this we deduce the definition in the graph sense which is a bit tricky:
. From this we deduce the definition in the graph sense which is a bit tricky: 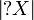 is the set of finite anticliques of X, and given two finite anticliques x and y of X we have
is the set of finite anticliques of X, and given two finite anticliques x and y of X we have 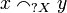 iff there is
iff there is 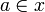 and
and 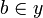 such that
such that 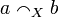 .
.
Note that both for the par and the why not it is much more convenient to define the strict coherence than the coherence.
With these two last constructions, the equation between the stable function space, the of course and the linear function space may be written:
.
One and bottom
Depending on the context we denote by 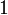 or
or 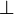 the coherent space whose web is a singleton and whose coherence relation is the trivial reflexive relation.
the coherent space whose web is a singleton and whose coherence relation is the trivial reflexive relation.
Theorem
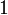 is neutral for tensor, that is, there is a linear isomorphism
is neutral for tensor, that is, there is a linear isomorphism 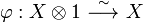 .
.
Similarly  is neutral for par.
is neutral for par.
Zero and top
Depending on the context we denote by  or
or 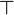 the coherent space with empty web.
the coherent space with empty web.
Theorem
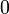 is neutral for the direct sum
is neutral for the direct sum 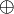 ,
, 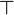 is neutral for the cartesian product
is neutral for the cartesian product 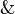 .
.
Remark:
It is one of the main defect of coherent semantics w.r.t. linear logic that it identifies the neutrals: in coherent semantics 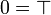 and
and 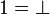 . However there is no known semantics of LL that solves this problem in a satisfactory way.
. However there is no known semantics of LL that solves this problem in a satisfactory way.
After coherent semantics
Coherent semantics was an important milestone in the modern theory of logic of programs, in particular because it leaded to the invention of Linear Logic, and more generally because it establishes a strong link between logic and linear algebra; this link is nowadays aknowledged by the customary use of monoidal categories in logic. In some sense coherent semantics is a precursor of many forthcoming works that explore the linear nature of logic as for example geometry of interaction which interprets proofs by operators or finiteness semantics which interprets formulas as vector spaces and resulted in differential linear logic...
Lots of this work have been motivated by the fact that coherent semantics is not complete as a semantics of programs (technically one says that it is not fully abstract). In order to see this, let us firts come back on the origin of the central concept of stability which as pointed above originated in the study of the sequentiality in programs.
Sequentiality
Sequentiality is a property that we will not define here (it would diserve its own article). We rely on the intuition that a function of n arguments is sequential if one can determine which of these argument is examined first during the computation. Obviously any function implemented in a functionnal language is sequential; for example the function or defined à la CAML by:
or = fun (x, y) -> if x then true else y
examines its argument x first. Note that this may be expressed more abstractly by the property: 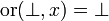 for any boolean x: the function or needs its first argument in order to compute anything. On the other hand we have
for any boolean x: the function or needs its first argument in order to compute anything. On the other hand we have 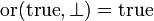 : in some case (when the first argument is true), the function doesn't need its second argument at all.
: in some case (when the first argument is true), the function doesn't need its second argument at all.
The typical non sequential function is the parallel or (that one cannot define in a CAML like language).
For a while one may have believed that the stability condition on which coherent semantics is built was enough to capture the notion of sequentiality of programs. A hint was the already mentionned fact that the parallel or is not stable. This diserves a bit of explanation.
The parallel or is not stable
Let B be the coherent space of booleans, also know as the flat domain of booleans: 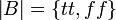 where tt and ff are two arbitrary distinct objects (for example one may take tt = 0 and ff = 1) and for any
where tt and ff are two arbitrary distinct objects (for example one may take tt = 0 and ff = 1) and for any 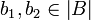 , define
, define 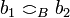 iff b1 = b2. Then B has exactly three cliques: the empty clique that we shall denote
iff b1 = b2. Then B has exactly three cliques: the empty clique that we shall denote 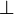 , the singleton {tt} that we shall denote T and the singleton {ff} that we shall denote F. These three cliques are ordered by inclusion:
, the singleton {tt} that we shall denote T and the singleton {ff} that we shall denote F. These three cliques are ordered by inclusion: 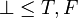 (we use
(we use 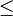 for
for 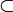 to enforce the idea that coherent spaces are domains).
to enforce the idea that coherent spaces are domains).
Recall the definition of the with, and in particular that any clique of 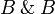 has the form
has the form 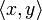 where x and y are cliques of B. Thus
where x and y are cliques of B. Thus 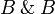 has 9 cliques:
has 9 cliques: 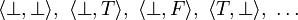 that are ordered by the product order:
that are ordered by the product order: 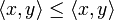 iff
iff 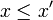 and
and 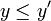 .
.
With these notations in mind one may define the parallel or by:
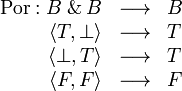
The function is completely determined if we add the assumption that it is non decreasing; for example one must have 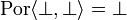 because the lhs has to be less than both T and F (because
because the lhs has to be less than both T and F (because 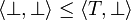 and
and 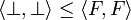 ).
).
The function is not stable because 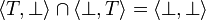 , thus
, thus 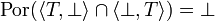 whereas
whereas 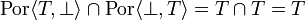 .
.
Another way to see this is: suppose x and y are two cliques of B such that 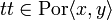 , which means that
, which means that 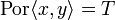 ; according to the caracterisation theorem of stable functions, if Por were stable then there would be a unique minimum x0 included in x, and a unique minimum y0 included in y such that
; according to the caracterisation theorem of stable functions, if Por were stable then there would be a unique minimum x0 included in x, and a unique minimum y0 included in y such that 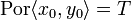 . This is not the case because both
. This is not the case because both 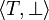 and
and 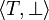 are minimal such that their value is T.
are minimal such that their value is T.
In other terms, knowing that 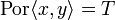 doesn't tell which of x of y is responsible for that, although we know by the definition of Por that only one of them is. Indeed the Por function is not representable in sequential programming languages such as (typed) lambda-calculus.
doesn't tell which of x of y is responsible for that, although we know by the definition of Por that only one of them is. Indeed the Por function is not representable in sequential programming languages such as (typed) lambda-calculus.
So the first genuine idea would be that stability caracterises sequentiality; but...
The Gustave function is stable
The Gustave function, so-called after an old joke, was found by Gérard Berry as an example of a function that is stable but non sequential. It is defined by:
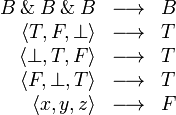
The last clause is for all cliques x, y and z such that 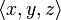 is incompatible with the three cliques
is incompatible with the three cliques 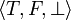 ,
, 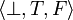 and
and 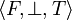 , that is such that the union with any of these three cliques is not a clique in
, that is such that the union with any of these three cliques is not a clique in 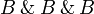 . We shall denote x1, x2 and x3 these three cliques.
. We shall denote x1, x2 and x3 these three cliques.
We furthemore assume that the Gustave function is non decreasing, so that we get 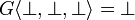 .
.
We note that x1, x2 and x3 are pairwise incompatible. From this we can deduce that the Gustave function is stable: typically if 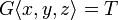 then exactly one of the xis is contained in
then exactly one of the xis is contained in 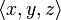 .
.
However it is not sequential because there is no way to determine which of its three arguments is examined first: it is not the first one otherwise we would have 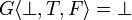 and similarly it is not the second one nor the third one.
and similarly it is not the second one nor the third one.
In other terms there is no way to implement the Gustave function by a lambda-term (or in any sequential programming language). Thus coherent semantics is not complete w.r.t. lambda-calculus.
The research for a right model for sequentiality was the motivation for lot of work, e.g., sequential algorithms by Gérard Bérry and Pierre-Louis Currien in the early eighties, that were more recently reformulated as a kind of game model, and the theory of hypercoherent spaces by Antonio Bucciarelli and Thomas Ehrhard.
Multiplicative neutrals and the mix rule
Coherent semantics is slightly degenerated w.r.t. linear logic because it identifies multiplicative neutrals (it also identifies additive neutrals but that's yet another problem): the coherent spaces 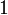 and
and 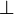 are equal.
are equal.
The first consequence of the identity 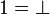 is that the formula
is that the formula 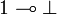 becomes provable, and so does the formula
becomes provable, and so does the formula 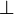 . Note that this doesn't entail (as in classical logic or intuitionnistic logic) that linear logic is incoherent because the principle
. Note that this doesn't entail (as in classical logic or intuitionnistic logic) that linear logic is incoherent because the principle 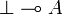 for any formula A is still not provable.
for any formula A is still not provable.
The equality 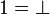 has also as consequence the fact that
has also as consequence the fact that 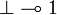 (or equivalently the formula
(or equivalently the formula 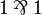 ) is provable. This principle is also known as the mix rule
) is provable. This principle is also known as the mix rule
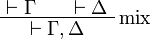
as it can be used to show that this rule is admissible:
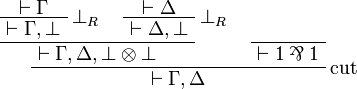
None of the two principles 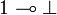 and
and 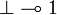 are valid in linear logic. To correct this one could extend the syntax of linear logic by adding the mix-rule. This is not very satisfactory as the mix rule violates some principles of Polarized linear logic, typically the fact that as sequent of the form
are valid in linear logic. To correct this one could extend the syntax of linear logic by adding the mix-rule. This is not very satisfactory as the mix rule violates some principles of Polarized linear logic, typically the fact that as sequent of the form 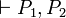 where P1 and P2 are positive, is never provable.
where P1 and P2 are positive, is never provable.
On the other hand the mix-rule is valid in coherent semantics so one could try to find some other model that invalidates the mix-rule. For example Girard's Coherent Banach spaces were an attempt to address this issue.
References
- ↑ Girard, Jean-Yves. The System F of Variable Types, Fifteen Years Later. Theoretical Computer Science. Volume 45, Issue 2, pp. 159-192, doi:10.1016/0304-3975(86)90044-7, 1986.