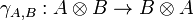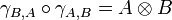Categorical semantics
| Line 1: | Line 1: | ||
| − | TODO: why categories? how to extract categorical models? etc. |
+ | Constructing denotational models of linear can be a tedious work. Categorical model are useful to identify the fundamental structure of these models, and thus simplify and make more abstract the elaboration of those models. |
| + | |||
| + | TODO: why categories? how to extract categorical models? etc. |
||
See <ref>{{BibEntry|bibtype=book|author=MacLane, Saunders|title=Categories for the Working Mathematician|publisher=Springer Verlag,year=1971,volume=5,series=Graduate Texts in Mathematics}}</ref>for a more detailed introduction to category theory. |
See <ref>{{BibEntry|bibtype=book|author=MacLane, Saunders|title=Categories for the Working Mathematician|publisher=Springer Verlag,year=1971,volume=5,series=Graduate Texts in Mathematics}}</ref>for a more detailed introduction to category theory. |
||
| Line 8: | Line 8: | ||
{{Definition|title=Monoidal category| |
{{Definition|title=Monoidal category| |
||
| − | A ''monoidal category'' <math>(\mathcal{C},\otimes,I)</math> is a category <math>\mathcal{C}</math> equipped with |
+ | A ''monoidal category'' <math>(\mathcal{C},\otimes,I,\alpha,\lambda,\rho)</math> is a category <math>\mathcal{C}</math> equipped with |
* a functor <math>\otimes:\mathcal{C}\times\mathcal{C}\to\mathcal{C}</math> called ''tensor product'', |
* a functor <math>\otimes:\mathcal{C}\times\mathcal{C}\to\mathcal{C}</math> called ''tensor product'', |
||
* an object <math>I</math> called ''unit object'', |
* an object <math>I</math> called ''unit object'', |
||
| − | * three natural isomorphisms of components |
+ | * three natural isomorphisms <math>\alpha</math>, <math>\lambda</math> and <math>\rho</math>, called respectively ''associator'', ''left unitor'' and ''right unitor'', whose components are |
: <math> |
: <math> |
||
\alpha_{A,B,C}:(A\otimes B)\otimes C\to A\otimes (B\otimes C) |
\alpha_{A,B,C}:(A\otimes B)\otimes C\to A\otimes (B\otimes C) |
||
| Line 19: | Line 19: | ||
\rho_A:A\otimes I\to A |
\rho_A:A\otimes I\to A |
||
</math> |
</math> |
||
| − | called respectively ''associator'', ''left unitor'' and ''right unitor'', |
||
| − | |||
such that |
such that |
||
* for every objects <math>A,B,C,D</math> in <math>\mathcal{C}</math>, the diagram |
* for every objects <math>A,B,C,D</math> in <math>\mathcal{C}</math>, the diagram |
||
| Line 38: | Line 36: | ||
:<math>\gamma_{B,A}\circ\gamma_{A,B}=A\otimes B</math> |
:<math>\gamma_{B,A}\circ\gamma_{A,B}=A\otimes B</math> |
||
for every objects <math>A</math> and <math>B</math>. |
for every objects <math>A</math> and <math>B</math>. |
||
| + | }} |
||
| + | |||
| + | == Modeling the additives == |
||
| + | {{Definition|title=Product| |
||
| + | }} |
||
| + | |||
| + | {{Definition|title=Monoid| |
||
| + | }} |
||
| + | |||
| + | {{Property| |
||
| + | Categories with products vs monoidal categories. |
||
}} |
}} |
||
Revision as of 19:40, 23 March 2009
Constructing denotational models of linear can be a tedious work. Categorical model are useful to identify the fundamental structure of these models, and thus simplify and make more abstract the elaboration of those models.
TODO: why categories? how to extract categorical models? etc.
See [1]for a more detailed introduction to category theory.
Contents |
Modeling IMLL
A model of IMLL is a closed symmetric monoidal category. We recall the definition of these categories below.
Definition (Monoidal category)
A monoidal category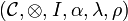 
is a category 
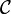equipped with
- a functor
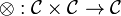called tensor product,
- an object I called unit object,
- three natural isomorphisms α, λ and ρ, called respectively associator, left unitor and right unitor, whose components are
such that
- for every objects A,B,C,D in , the diagram
commutes,
- for every objects A and B in , the diagrams
commute.
Definition (Braided, symmetric monoidal category)
A braided monoidal category is a category together with a natural isomorphism of components
called braiding, such that the two diagrams
- UNIQ5bed6f261dfbca91-math-00000011-QINU
commute for every objects A, B and C.
A symmetric monoidal category is a braided monoidal category in which the braiding satisfies
for every objects A and B.
Modeling the additives
Definition (Product)
Definition (Monoid)
Property
Categories with products vs monoidal categories.
Modeling IMALL
Modeling negation
Definition (*-autonomous category)
TODO
References
- ↑ MacLane, Saunders. Categories for the Working Mathematician.
