Game semantics
From LLWiki
Revision as of 18:28, 2 February 2009 by Pierre Clairambault (Talk | contribs)
This article presents the game-theoretic fully complete model of MLL. Formulas are interpreted by games between two players, Player and Opponent, and proofs are interpreted by strategies for Player.
Preliminary definitions and notations
- If M is a set, M * will denote the set of finite words on M;
- If
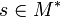 , | s | will denote the length of s;
, | s | will denote the length of s;
- If
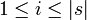 , si will denote the i-th move of s;
, si will denote the i-th move of s;
- We define
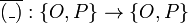 with
with 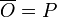 and
and 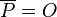
- We denote by
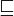 the prefix partial order on M *
the prefix partial order on M *
Games and Strategies
Definition (Games)
A game A is a triple (MA,λA,PA) where:
- MA is a finite set of moves;
-
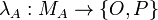 is a polarity function;
is a polarity function;
- PA is a subset of
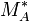 such that
such that
- Each
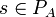 is alternated, i.e. if we define λA(si) = Q then, if defined,
is alternated, i.e. if we define λA(si) = Q then, if defined, 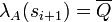 ;
;
- A is finite: there is no infinite strictly increasing sequence
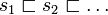 in PA.
in PA.
- Each