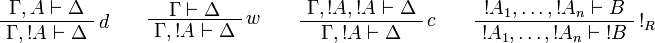Sequent calculus
This article presents the language and sequent calculus of second-order propositional linear logic and the basic properties of this sequent calculus.
Contents |
Formulas
Formulas are built on a set of atoms, written 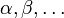 , that can
be either propositional variables
, that can
be either propositional variables 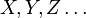 or atomic formulas
or atomic formulas
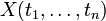 , where the ti are terms from some first-order language.
Formulas, represented by capital letters A, B, C, are built using the
following connectives:
, where the ti are terms from some first-order language.
Formulas, represented by capital letters A, B, C, are built using the
following connectives:
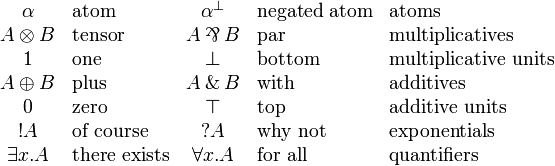
Each line corresponds to a particular class of connectives, and each class
consists in a pair of connectives.
Those in the left column are called positive and those in the right column are
called negative.
The tensor and with are conjunctions while par and
plus are disjunctions.
The exponential connectives are called modalities, and traditionally
read of course A for 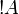 and why not A for
and why not A for 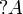 .
Quantifiers may apply to first- or second-order variables.
.
Quantifiers may apply to first- or second-order variables.
Given a formula A, its linear negation, also called orthogonal and
written 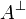 , is obtained by exchanging each positive connective with the
negative one of the same class and vice versa, in a way analogous to de Morgan
laws in classical logic.
Formally, the definition of linear negation is
, is obtained by exchanging each positive connective with the
negative one of the same class and vice versa, in a way analogous to de Morgan
laws in classical logic.
Formally, the definition of linear negation is
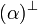
|
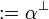
|
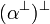
|
: = α |
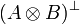
|
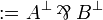
|
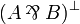
|
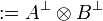
|
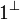
|
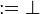
|
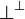
|
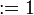
|
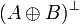
|
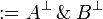
|
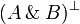
|
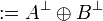
|
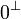
|
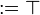
|
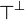
|
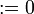
|
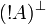
|
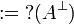
|
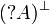
|
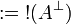
|
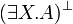
|
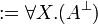
|
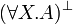
|
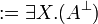
|
Note that this operation is defined syntactically, hence negation is not a
connective, the only place in formulas where the symbol 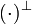 occurs
is for negated atoms
occurs
is for negated atoms 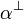 .
Note also that, by construction, negation is involutive: for any formula A,
it holds that
.
Note also that, by construction, negation is involutive: for any formula A,
it holds that 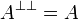 .
.
There is no connective for implication in the syntax of standard linear logic.
Instead, a linear implication is defined similarly to the decomposition
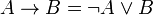 in classical logic:
in classical logic:
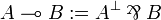
Free and bound variables are defined in the standard way, as well as
substitution.
Formulas are always considered up to renaming of bound names.
If A and B are formulas and X is a propositional variable, the formula
A[B / X] is A where all atoms X are replaced (without capture) by B and
all atoms 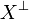 are replaced by the formula
are replaced by the formula 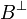 .
.
Sequents and proofs
A sequent is an expression 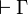 where Γ is a finite multiset
of formulas.
For a multiset
where Γ is a finite multiset
of formulas.
For a multiset 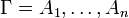 , the notation
, the notation 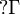 represents
the multiset
represents
the multiset 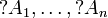 .
Proofs are labelled trees of sequents, built using the following inference
rules:
.
Proofs are labelled trees of sequents, built using the following inference
rules:
- Identity group:
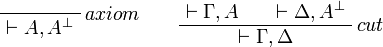
- Multiplicative group:
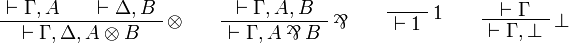
- Additive group:
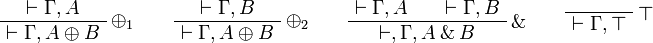
- Exponential group:
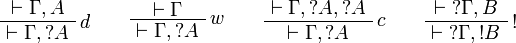
- Quantifier group (in the
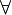 rule, X must not occur in Γ):
rule, X must not occur in Γ):
![\AxRule{ \vdash \Gamma, A[B/X] }
\LabelRule{ \exists }
\UnaRule{ \vdash \Gamma, \exists X.A }
\DisplayProof
\qquad
\AxRule{ \vdash \Gamma, A }
\LabelRule{ \forall }
\UnaRule{ \vdash \Gamma, \forall X.A }
\DisplayProof](/mediawiki/images/math/1/e/6/1e6c32e0048d367f11036be5492e2946.png)
The rules for exponentials are called dereliction, weakening,
contraction and promotion, respectively.
Note the fundamental fact that there are no contraction and weakening rules
for aribtrary formulas, but only for the formulas starting with the 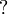 modality.
This is what distinguishes linear logic from classical logic: if weakening and
contraction were allowed for arbitrary formulas, then
modality.
This is what distinguishes linear logic from classical logic: if weakening and
contraction were allowed for arbitrary formulas, then 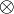 and
and 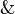 would be identified, as well as
would be identified, as well as 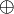 and
and 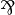 ,
, 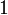 and
and 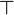 ,
,
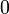 and
and 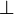 .
By identified, we mean here that replacing a
.
By identified, we mean here that replacing a 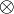 with a
with a 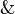 or
vice versa would preserve provability.
or
vice versa would preserve provability.
Note that this system contains only introduction rules and no elimination
rule.
Moreover, there is no introduction rule for the additive unit 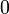 , the
only ways to introduce it at top level are the axiom rule and the
, the
only ways to introduce it at top level are the axiom rule and the 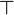 rule.
rule.
Sequents are considered as multisets, in other words as sequences up to permutation. An equivalent presentation would be to define a sequent as a finite sequence of formulas and to add the exchange rule:
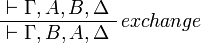
Equivalences and definability
Two formulas A and B are (linearly) equivalent, written 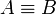 , if
both implications
, if
both implications 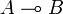 and
and 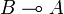 are provable.
Equivalently,
are provable.
Equivalently, 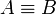 if both
if both 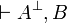 and
and 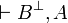 are provable.
Another formulation of
are provable.
Another formulation of 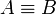 is that, for all Γ,
is that, for all Γ,
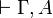 is provable if and only if
is provable if and only if 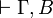 is provable.
Note that, because of the definition of negation, an equivalence
is provable.
Note that, because of the definition of negation, an equivalence
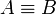 holds if and only if the dual equivalence
holds if and only if the dual equivalence
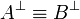 holds.
holds.
Fundamental equivalences
- Associativity, commutativity, neutrality:
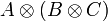
|
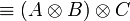
|
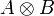
|
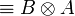
|
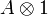
|
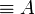
|
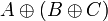
|
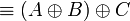
|
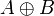
|
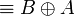
|
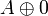
|
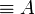
|
- Idempotence of additives:
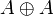
|
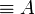
|
- Distributivity of multiplicatives over additives:
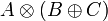
|
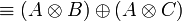
|
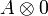
|
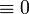
|
- Defining property of exponentials:
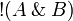
|
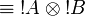
|
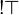
|
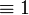
|
- Monoidal structure of exponentials, digging:
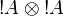
|
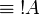
|
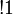
|
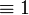
|

|
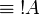
|
- Commutation of quantifiers (z does not occur in A):
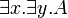
|
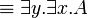
|
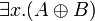
|
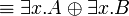
|
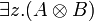
|
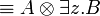
|
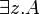
|
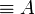
|
Definability
The units and the additive connectives can be defined using second-order quantification and exponentials, indeed the following equivalences hold:
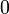
|
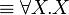
|
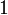
|
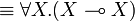
|
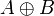
|
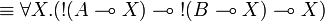
|
Any pair of connectives that has the same rules as 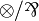 is
equivalent to it, the same holds for additives, but not for exponentials.
is
equivalent to it, the same holds for additives, but not for exponentials.
Positive/negative commutation
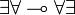 ,
,
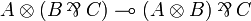
Properties of proofs
The fundamental property of the sequent calculus of linear logic is the cut elimination property, which states that the cut rule is useless as far as provability is concerned. This property is exposed in the following section, together with a sketch of proof.
Cut elimination and consequences
Theorem (cut elimination)
For every sequent 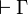 , there is a proof of
, there is a proof of 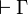 if and
only if there is a proof of
if and
only if there is a proof of 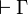 that does not use the cut rule.
that does not use the cut rule.
This property is proved using a set of rewriting rules on proofs, using appropriate termination arguments (see the specific articles on cut elimination for detailed proofs), it is the core of the proof/program correspondence.
It has several important consequences:
Definition (subformula)
The subformulas of a formula A are A and, inductively, the subformulas of its immediate subformulas:
- the immediate subformulas of
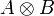 ,
, 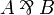 ,
, 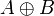 ,
,
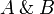 are A and B,
are A and B,
- the only immediate subformula of
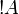 and
and 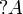 is A,
is A,
-
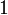 ,
, 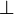 ,
, 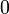 ,
, 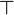 and atomic formulas α and
and atomic formulas α and
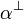 have no immediate subformula,
have no immediate subformula,
- the immediate subformulas of
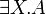 and
and 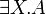 are all
are all
the A[B / X] for all formulas B.
Theorem (subformula property)
A sequent 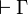 is provable if and only if it is the conclusion of
a proof in which each intermediate conclusion is made of subformulas of the
formulas of Γ.
is provable if and only if it is the conclusion of
a proof in which each intermediate conclusion is made of subformulas of the
formulas of Γ.
Proof.
By the cut elimination theorem, if a sequent 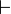 is provable, then it
is provable by a cut-free proof.
In each rule except the cut rule, all formulas of the premisses are either
formulas of the conclusion, or immediate subformulas of it, therefore
cut-free proofs have the subformula property.
is provable, then it
is provable by a cut-free proof.
In each rule except the cut rule, all formulas of the premisses are either
formulas of the conclusion, or immediate subformulas of it, therefore
cut-free proofs have the subformula property.
The subformula property means essentially nothing in the second-order system, since any formula is a subformula of a quantified formula where the quantified variable occurs. However, the property is very meaningful if the sequent Γ does not use second-order quantification, as it puts a strong restriction on the set of potential proofs of a given sequent. In particular, it implies that the first-order fragment without quantifiers is decidable.
Theorem (consistency)
The empty sequent 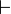 is not provable.
Subsequently, it is impossible to prove both a formula A and its negation
is not provable.
Subsequently, it is impossible to prove both a formula A and its negation
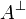 ; it is impossible to prove
; it is impossible to prove 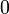 or
or 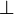 .
.
Proof.
If 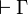 is a provable sequent, then it is the conclusion of a
cut-free proof.
In each rule except the cut rule, there is at least one formula in
conclusion.
Therefore
is a provable sequent, then it is the conclusion of a
cut-free proof.
In each rule except the cut rule, there is at least one formula in
conclusion.
Therefore 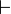 cannot be the conclusion of a proof.
cannot be the conclusion of a proof.
The other properties are immediate consequences: if A and 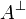 were
provable, then by a cut rule one would get an empty conclusion, which is not
possible.
As particular cases, since
were
provable, then by a cut rule one would get an empty conclusion, which is not
possible.
As particular cases, since 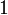 and
and 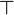 are provable, their negations
are provable, their negations
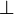 and
and 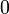 are not.
are not.
Expansion of identities
Let us write 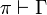 to signify that π is a proof with
conclusion
to signify that π is a proof with
conclusion 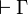 .
.
Proposition (η-expansion)
For every proof π, there is a proof π' with the same conclusion as
π in which the axiom rule is only used with atomic formulas.
If π is cut-free, then there is a cut-free π'.
Proof.
It suffices to prove that for every formula A, the sequent
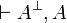 has a cut-free proof in which the axiom rule is used only
for atomic formulas.
We prove this by induction on A.
Not that there is a case for each pair of dual connectives.
has a cut-free proof in which the axiom rule is used only
for atomic formulas.
We prove this by induction on A.
Not that there is a case for each pair of dual connectives.
- If A is atomic, then
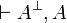 is an instance of the atomic
is an instance of the atomic
axiom rule.
- If
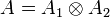 then we have
then we have
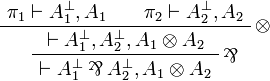
where π1 and π2 exist by induction hypothesis.
- If
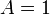 or
or 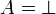 then we have
then we have
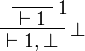
- If
 then we have
then we have
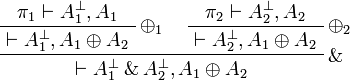
where π1 and π2 exist by induction hypothesis.
- If
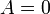 or
or 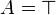 , we have
, we have
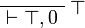
- If
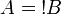 then we have
then we have
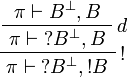
where π exists by induction hypothesis.
- If
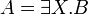 then we have
then we have
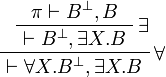
where π exists by induction hypothesis.
The interesting thing with η-expansion is that, we can always assume that
each connective is explicitly introduced by its associated rule (except in the
case where there is an occurrence of the 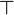 rule).
rule).
Reversibility
Definition (reversibility)
A connective c is called reversible if
- for every proof
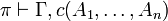 , there is a proof
, there is a proof
π' with the same conclusion in which 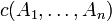 is introduced
by the last rule,
is introduced
by the last rule,
- if π is cut-free then there is a cut-free π'.
Proposition
The connectives  ,
, 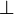 ,
, 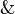 ,
, 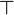 and
and 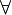 are
reversible.
are
reversible.
Proof.
Using the η-expansion property, we assume that the axiom rule is only
applied to atomic formulas.
Then each top-level connective is introduced either by its associated rule
or in an instance of the 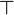 rule.
rule.
For 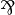 , consider a proof
, consider a proof 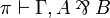 .
If
.
If 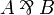 is introduced by a
is introduced by a 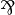 rule, then if we remove this rule
we get a proof of
rule, then if we remove this rule
we get a proof of 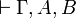 (this can be proved by a
straightforward induction).
If it is introduced in the contect of a
(this can be proved by a
straightforward induction).
If it is introduced in the contect of a 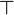 rule, then this rule can be
changed so that
rule, then this rule can be
changed so that 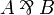 is replaced by A,B.
In either case, we can apply a final
is replaced by A,B.
In either case, we can apply a final 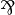 rule to get the expected proof.
rule to get the expected proof.
For 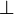 , the same technique applies: if it is introduced by a
, the same technique applies: if it is introduced by a 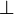 rule, then remove this rule to get a proof of
rule, then remove this rule to get a proof of 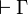 , if it is
introduced by a
, if it is
introduced by a 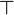 rule, remove the
rule, remove the 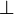 from this rule, then apply
the
from this rule, then apply
the 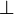 rule at the end of the new proof.
rule at the end of the new proof.
For 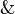 , consider a proof
, consider a proof 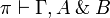 .
If the connective is introduced by a
.
If the connective is introduced by a 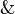 rule then this rule is applied
in a context like
rule then this rule is applied
in a context like
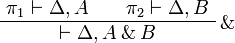
Since the formula 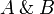 is not involved in other rules (except as
context), if we replace this step by π1 in π we finally get a proof
is not involved in other rules (except as
context), if we replace this step by π1 in π we finally get a proof
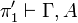 .
If we replace this step by π2 we get a proof
.
If we replace this step by π2 we get a proof 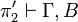 .
Combining π1 and π2 with a final
.
Combining π1 and π2 with a final 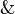 rule we finally get the
expected proof.
The case when the
rule we finally get the
expected proof.
The case when the 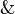 was introduced in a
was introduced in a 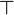 rule is solved as
before.
rule is solved as
before.
For 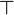 the result is trivial: just choose π' as an instance of the
the result is trivial: just choose π' as an instance of the
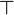 rule with the appropriate conclusion.
rule with the appropriate conclusion.
For 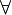 , consider a proof
, consider a proof 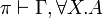 .
Up to renaming, we can assume that X occurs free only above the rule that
introduces the quantifier.
If the quantifier is introduced by a
.
Up to renaming, we can assume that X occurs free only above the rule that
introduces the quantifier.
If the quantifier is introduced by a 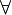 rule, then if we remove this
rule, we can check that we get a proof of
rule, then if we remove this
rule, we can check that we get a proof of 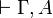 on which we can
finally apply the
on which we can
finally apply the 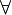 rule.
The case when the
rule.
The case when the 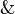 was introduced in a
was introduced in a 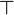 rule is solved as
before.
rule is solved as
before.
Note that, in each case, if the proof we start from is cut-free, our
transformations do not introduce a cut rule.
However, if the original proof has cuts, then the final proof may have more
cuts, since in the case of 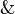 we duplicated a part of the original
proof.
we duplicated a part of the original
proof.
Variations
Two-sided sequent calculus
The sequent calculus of linear logic can also be presented using two-sided
sequents 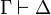 , with any number of formulas on the left and
right.
In this case, it is customary to provide rules only for the positive
connectives, then there are left and right introduction rules and a negation
rule that moves formulas between the left and right sides:
, with any number of formulas on the left and
right.
In this case, it is customary to provide rules only for the positive
connectives, then there are left and right introduction rules and a negation
rule that moves formulas between the left and right sides:
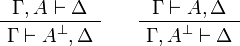
Identity group:
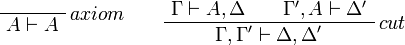
Multiplicative group:
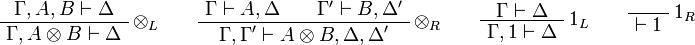
Additive group:
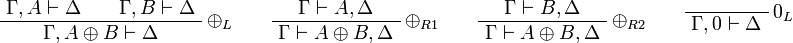
Exponential group: