Intuitionistic linear logic
Intuitionistic Linear Logic (ILL) is the
intuitionnistic restriction of linear logic: the sequent calculus
of ILL is obtained from the two-sided sequent calculus of
linear logic by constraining sequents to have exactly one formula on
the right-hand side: 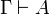 .
.
The connectives 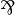 ,
, 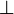 and
and 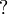 are
not available anymore, but the linear implication
are
not available anymore, but the linear implication 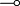 is.
is.
Sequent Calculus
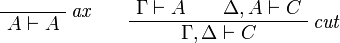
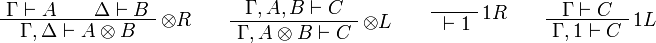
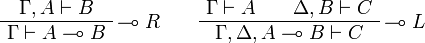
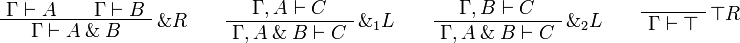
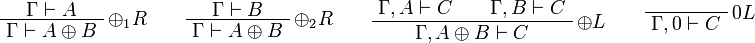
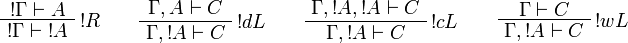
![\AxRule{\Gamma\vdash A}
\LabelRule{\forall R}
\UnaRule{\Gamma\vdash \forall\alpha A}
\DisplayProof
\qquad
\AxRule{\Gamma,A[\tau/\alpha]\vdash C}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\alpha A\vdash C}
\DisplayProof
\qquad
\AxRule{\Gamma\vdash A[\tau/\alpha]}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash\exists\alpha A}
\DisplayProof
\qquad
\AxRule{\Gamma,A\vdash C}
\LabelRule{\exists L}
\UnaRule{\Gamma,\exists\alpha A\vdash C}
\DisplayProof](/mediawiki/images/math/a/9/5/a95dbb5013cc708c2470ee8327494607.png)
with α not free in Γ,C in the rules 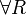 and
and 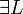 .
.
The intuitionistic fragment of linear logic
In order to characterize intuitionistic linear logic inside linear logic, we define the intuitionistic restriction of linear formulas:
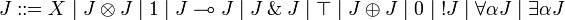
JLL is the fragment of linear logic obtained by restriction to intuitionistic formulas.
Theorem (JLL and ILL)
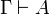 is provable in ILL1 if and only if it is provable in JLL1.
is provable in ILL1 if and only if it is provable in JLL1.
Proof. The first direction is immediate since ILL1 is included in JLL1.
For the second direction, we consider a cut-free proof of 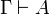 in JLL1. We prove by induction on the length of such a proof that it belongs to ILL1.
in JLL1. We prove by induction on the length of such a proof that it belongs to ILL1.
This result is still valid with units from ILL1 into JLL1. In the opposite direction, it holds with 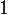 but not anymore with
but not anymore with 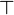 and
and 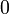 .
. 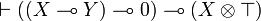 is provable in JLL1:
is provable in JLL1:
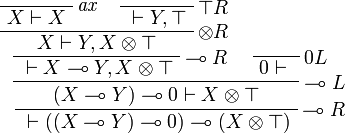
but not in ILL1.