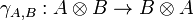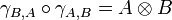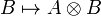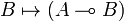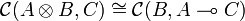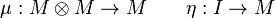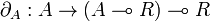Categorical semantics
Constructing denotational models of linear can be a tedious work. Categorical semantics are useful to identify the fundamental structure of these models, and thus simplify and make more abstract the elaboration of those models.
TODO: why categories? how to extract categorical models? etc.
See [1]for a more detailed introduction to category theory. See [2]for a detailed treatment of categorical semantics of linear logic.
Contents |
Modeling IMLL
A model of IMLL is a closed symmetric monoidal category. We recall the definition of these categories below.
Definition (Monoidal category)
A monoidal category 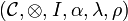 is a category
is a category 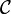 equipped with
equipped with
- a functor
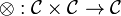 called tensor product,
called tensor product,
- an object I called unit object,
- three natural isomorphisms α, λ and ρ, called respectively associator, left unitor and right unitor, whose components are
such that
- for every objects A,B,C,D in
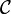 , the diagram
, the diagram
- TODO
commutes,
- for every objects A and B in
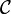 , the diagrams
, the diagrams
- TODO
commute.
Definition (Braided, symmetric monoidal category)
A braided monoidal category is a category together with a natural isomorphism of components
called braiding, such that the two diagrams
- UNIQ576ba9877b6412cc-math-00000016-QINU
commute for every objects A, B and C.
A symmetric monoidal category is a braided monoidal category in which the braiding satisfies
for every objects A and B.
Definition (Closed monoidal category)
A monoidal category 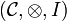 is left closed when for every object A, the functor
is left closed when for every object A, the functor
has a right adjoint, written
This means that there exists a bijection
which is natural in B and C. Equivalently, a monoidal category is left closed when it is equipped with a left closed structure, which consists of
- an object
 ,
,
- a morphism
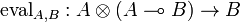 , called left evaluation,
, called left evaluation,
for every objects A and B, such that for every morphism 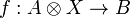 there exists a unique morphism
there exists a unique morphism 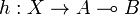 making the diagram
making the diagram
- TODO
commute.
Dually, the monoidal category 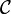 is right closed when the functor
is right closed when the functor 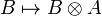 admits a right adjoint. The notion of right closed structure can be defined similarly.
admits a right adjoint. The notion of right closed structure can be defined similarly.
In a symmetric monoidal category, a left closed structure induces a right closed structure and conversely, allowing us to simply speak of a closed symmetric monoidal category.
Modeling the additives
Definition (Product)
A category has finite products when it has products and a terminal object.
Definition (Monoid)
A monoid (M,μ,η) in a monoidal category 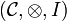 is an object M together with two morphisms
is an object M together with two morphisms
such that the diagrams
- TODO
commute.
Property
Categories with products vs monoidal categories.
Modeling ILL
Introduced in[3].
Definition (Linear-non linear (LNL) adjunction)
A linear-non linear adjunction is a symmetric monoidal adjunction between lax monoidal functors
in which the category 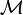 has finite products.
has finite products.
Modeling negation
*-autonomous categories
Definition (*-autonomous category)
Suppose that we are given a symmetric monoidal closed category 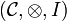 and an object R of
and an object R of 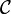 . For every object A, we define a morphism
. For every object A, we define a morphism
as follows. By applying the bijection of the adjunction defining (left) closed monoidal categories to the identity morphism 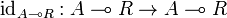 , we get a morphism
, we get a morphism 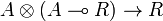 , and thus a morphism
, and thus a morphism 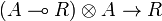 by precomposing with the symmetry
by precomposing with the symmetry 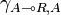 . The morphism
. The morphism 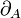 is finally obtained by applying the bijection of the adjunction defining (left) closed monoidal categories to this morphism. The object R is called dualizing when the morphism
is finally obtained by applying the bijection of the adjunction defining (left) closed monoidal categories to this morphism. The object R is called dualizing when the morphism 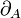 is a bijection for every object A of
is a bijection for every object A of 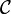 . A symmetric monoidal closed category is *-autonomous when it admits such a dualizing object.
. A symmetric monoidal closed category is *-autonomous when it admits such a dualizing object.
Compact closed categories
Definition (Compact closed category)
A symmetric monoidal category 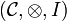 is compact closed when every object A has a (left) dual.
is compact closed when every object A has a (left) dual.
In a compact closed category the left and right duals of an object A are isomorphic.
Property
A compact closed category is monoidal closed.