Reversibility and focalization
(Creation) |
Revision as of 22:10, 31 August 2012
Reversibility
Theorem
Negative connectives are reversible:
- A sequent
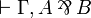 is provable if and only if
is provable if and only if 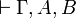 is provable.
is provable.
- A sequent
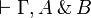 is provable if and only if
is provable if and only if 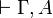 and
and 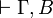 are provable.
are provable.
- A sequent
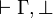 is provable if and only if
is provable if and only if 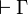 is provable.
is provable.
- A sequent
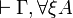 is provable if and only if
is provable if and only if 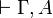 is provable, for some fresh variable ξ.
is provable, for some fresh variable ξ.
Proof.
We start with the case of the 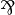 connective.
If
connective.
If 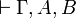 is provable, then by the introduction rule for
is provable, then by the introduction rule for 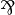 we know that
we know that 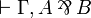 is provable.
For the reverse implication we proceed by induction on a proof π of
is provable.
For the reverse implication we proceed by induction on a proof π of
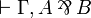 .
.
- If the last rule of π is the introduction of the
 in
in 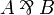 , then the premiss is exacty
, then the premiss is exacty 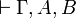 so we can conclude.
so we can conclude.
- The other case where the last rule introduces
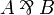 is when π is an axiom rule, hence
is when π is an axiom rule, hence 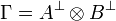 . Then we can conclude with the proof
. Then we can conclude with the proof
- Otherwise
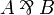 is in the context of the last rule. If the last rule is a tensor, then π has the shape
is in the context of the last rule. If the last rule is a tensor, then π has the shape
- or the same with
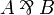 in the conclusion of π2 instead. By induction hypothesis on π1 we get a proof π'1 of
in the conclusion of π2 instead. By induction hypothesis on π1 we get a proof π'1 of 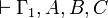 , then we can conclude with the proof
, then we can conclude with the proof
- The case of the cut rule has the same structure as the tensor rule.
- In the case of the
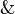 rule, we have
rule, we have 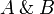 in both premisses and we conclude similarly, using the induction hypothesis on both π1 and π2.
in both premisses and we conclude similarly, using the induction hypothesis on both π1 and π2.
- If
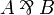 is in the context of a rules for
is in the context of a rules for 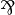 ,
, 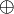 ,
, 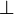 or quantifiers, or in the context of a dereliction, weakening or contraction, the situation is similar as for
or quantifiers, or in the context of a dereliction, weakening or contraction, the situation is similar as for 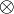 except that we have only one premiss.
except that we have only one premiss.
- If
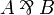 is in the context of
is in the context of 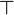 rules, we can freely change the context of the rule to get the expected one.
rules, we can freely change the context of the rule to get the expected one.
- The two remaining cases are if the last rule is the rule for 1 or a promotion. By the constraints these rules impose on the contexts, these cases cannot happen.
The 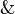 connective is treated in the same way.
In this cases where
connective is treated in the same way.
In this cases where 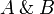 is in the context of a rule with two
premisses, the premiss where this formula is not present will be duplicated,
with one copy in the premiss for A and one in the premiss for B.
is in the context of a rule with two
premisses, the premiss where this formula is not present will be duplicated,
with one copy in the premiss for A and one in the premiss for B.
The 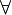 connective is also treated similarly.
Its peculiarity is that introducing
connective is also treated similarly.
Its peculiarity is that introducing 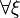 requires that ξ does
not appear free in the context.
For all rules with one premiss except the quantifier rules, the set of fresh
variables in the same in the premiss and the conclusion, so everything works
well.
Other rules might change the set of free variables, but problems are avoided
by choosing for ξ a variable that is fresh for the whole proof we are
considering.
requires that ξ does
not appear free in the context.
For all rules with one premiss except the quantifier rules, the set of fresh
variables in the same in the premiss and the conclusion, so everything works
well.
Other rules might change the set of free variables, but problems are avoided
by choosing for ξ a variable that is fresh for the whole proof we are
considering.
Remark that this result is proved using only commutation rules, except when the formula is introduced by an axiom rule. Furthermore, if axioms are applied only on atoms, this particular case disappears.
A consequence of this fact is that, when searching for a proof of some
sequent 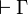 , one can always start by decomposing negative
connectives in Γ without losing provability.
Applying this result to successive connectives, we can get generalized
formulations for more complex formulas. For instance:
, one can always start by decomposing negative
connectives in Γ without losing provability.
Applying this result to successive connectives, we can get generalized
formulations for more complex formulas. For instance:
-
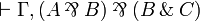 is provable
is provable
- iff
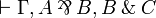 is provable
is provable
- iff
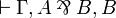 and
and 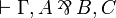 are provable
are provable
- iff
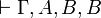 and
and 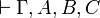 are provable
are provable
So without loss of generality, we can assume that any proof of
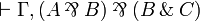 ends like
ends like
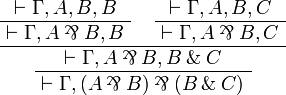
In order to define a general statement for compound formulas, as well as an analogous result for positive connectives, we need to give a proper status to clusters of connectives of the same polarity.
Generalized connectives and rules
Definition
A positive generalized connective is a parametrized formula
![P[X_1,\ldots,X_n]](/mediawiki/images/math/5/3/c/53c59e9f87f7cfc50ed7d4ef45d66c64.png) made from the variables Xi using the connectives
made from the variables Xi using the connectives
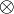 ,
, 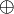 ,
, 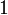 ,
, 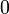 .
.
A negative generalized connective is a parametrized formula
![N[X_1,\ldots,X_n]](/mediawiki/images/math/0/1/3/013f9a4a6734c8d6526b785f75c2020a.png) made from the variables Xi using the connectives
made from the variables Xi using the connectives
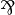 ,
, 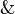 ,
, 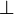 ,
, 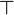 .
.
If ![C[X_1,\ldots,X_n]](/mediawiki/images/math/8/2/6/8261780451b451bed29f8467761447b6.png) is a generalized connectives (of any polarity), the
dual of C is the connective C * such that
is a generalized connectives (of any polarity), the
dual of C is the connective C * such that
![C^*[X_1\orth,\ldots,X_n\orth]=C[X_1,\ldots,X_n]\orth](/mediawiki/images/math/e/f/c/efc5e05d054dbc900f94fe0049e95e8f.png) .
.
It is clear that dualization of generalized connectives is involutive and exchanges polarities. We do not include quantifiers in this definition, mainly for simplicity. Extending the notion to quantifiers would only require taking proper care of the scope of variables.
Sequent calculus provides introduction rules for each connective. Negative
connectives have one rule, positive ones may have any number of rules, namely
2 for  and 0 for
and 0 for  . We can derive introduction rules for the
generalized connectives by combining the different possible introduction rules
for each of their components.
. We can derive introduction rules for the
generalized connectives by combining the different possible introduction rules
for each of their components.
Considering the previous example
![N[X_1,X_2,X_3]=(X_1\parr X_2)\parr(X_2\with X_3)](/mediawiki/images/math/d/7/a/d7aa2463d8253b8e209df73e22c6473c.png) , we can derive an
introduction rule for N as
, we can derive an
introduction rule for N as

but these rules only differ by the commutation of independent rules.
In particular, their premisses are the same.
The dual of N is ![P[X_1,X_2,X_3]=(X_1\tens X_2)\tens(X_2\plus X_3)](/mediawiki/images/math/b/5/7/b57987a548d09ca81d8fc03b4e99283e.png) , for
which we have two possible derivations:
, for
which we have two possible derivations:
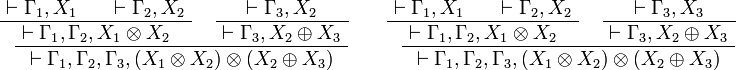
These are actually different, in particular their premisses differ.
Each possible derivation corresponds to the choice of one side of the  connective.
connective.
We can remark that the branches of the negative inference precisely correspond to the possible positive inferences:
- the first branch of the negative inference has a premiss X1,X2,X2 and the first positive inference has three premisses, holding X1, X2 and X2 respectively.
- the second branch of the negative inference has a premiss X1,X2,X3 and the second positive inference has three premisses, holding X1, X2 and X3 respectively.
This phenomenon extends to all generalized connectives.
Definition
The branching of a generalized connective ![P[X_1,\ldots,X_n]](/mediawiki/images/math/5/3/c/53c59e9f87f7cfc50ed7d4ef45d66c64.png) is the
multiset
is the
multiset 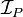 of multisets over
of multisets over 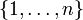 defined
inductively as
defined
inductively as
{
In the example above, the branching will be [[1,2,2],[1,2,3]], which corresponds to the granches of the negative inference and to the cases of positive inference.
Definition
Let 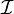 be a branching.
Write
be a branching.
Write 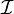 as
as ![[I_1,\ldots,I_k]](/mediawiki/images/math/1/9/c/19c5a0b0aa2e25c73fb18d6562fc0a6e.png) and write each Ij as
and write each Ij as
![[i_{j,1},\ldots,i_{j,\ell_j}]](/mediawiki/images/math/c/d/a/cda29a3ad88ab805686e7870e021bb4a.png) .
The derived rule for a negative generalized connective N with
branching
.
The derived rule for a negative generalized connective N with
branching 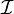 is
is
![\AxRule{ \vdash \Gamma, A_{i_{1,1}}, \ldots, A_{i_{1,\ell_1}} }
\AxRule{ \cdots }
\AxRule{ \vdash \Gamma, A_{i_{k,1}}, \ldots, A_{i_{k,\ell_k}} }
\LabelRule{N}
\TriRule{ \vdash \Gamma, N[A_1,\ldots,A_n] }
\DisplayProof](/mediawiki/images/math/1/f/5/1f55e46fa38e9fa1971fd9aeb24744f6.png)
For each branch ![I=[i_1,\ldots,i_\ell]](/mediawiki/images/math/3/6/a/36a7aefd1f6e18264946ad50ffff35aa.png) of a positive generalized connective
P, the derived rule for branch I of P is
of a positive generalized connective
P, the derived rule for branch I of P is
![\AxRule{ \vdash \Gamma_1, A_{i_1} }
\AxRule{ \cdots }
\AxRule{ \vdash \Gamma_\ell, A_{i_\ell} }
\LabelRule{P_I}
\TriRule{ \vdash \Gamma_1, \ldots, \Gamma_\ell, P[A_1,\ldots,A_n] }
\DisplayProof](/mediawiki/images/math/5/e/6/5e695e7d28ca8dff69b69577d1c618e4.png)
The reversibility property of negative connectives can be rephrased in a generalized way as
Theorem
Let N be a negative generalized connective. A sequent
![\vdash\Gamma,N[A_1,\ldots,A_n]](/mediawiki/images/math/9/3/2/93250e179a39054c9ae2cf7705817597.png) is provable if and only if, for each
is provable if and only if, for each
![[i_1,\ldots,i_k]\in\mathcal{I}_N](/mediawiki/images/math/f/3/5/f35869f3d326b4c5b569b5dadf3b3e9b.png) , the sequent
, the sequent
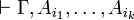 is provable.
is provable.
The corresponding property for positive connectives is the focalization property, defined in the next section.
Focalization
Definition
A formula is positive if it has a main connective among
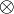 ,
, 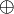 ,
, 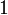 ,
, 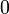 .
It is called negative if it has a main connective among
.
It is called negative if it has a main connective among
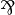 ,
, 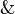 ,
, 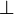 ,
, 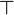 .
It is called neutral if it is neither positive nor negative.
.
It is called neutral if it is neither positive nor negative.
If we extended the theory to include quantifiers in generalized connectives, then the definition of positive and negative formulas would be extended to include them too.
Definition
A proof 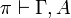 is said to be focalized on A if it has
the shape
is said to be focalized on A if it has
the shape
![\AxRule{ \pi_1 \vdash \Gamma_1, A_{i_1} }
\AxRule{ \cdots }
\AxRule{ \pi_\ell \vdash \Gamma_\ell, A_{i_\ell} }
\LabelRule{P_{[i_1,\ldots,i_\ell]}}
\TriRule{ \vdash \Gamma_1, \ldots, \Gamma_\ell, P[A_1,\ldots,A_n] }
\DisplayProof](/mediawiki/images/math/f/8/2/f82ccf20c32519ed9172728ea91db2e3.png)
where P is a positive generalized connective, the Ai ar non-positive
and ![A=P[A_1,\ldots,A_n]](/mediawiki/images/math/d/4/a/d4abc8edf8e44a554165ecf6ed3f0925.png) . The formula A is called the focus of the
proof π.
. The formula A is called the focus of the
proof π.
In other words, a proof is focalized on a conclusion A if its last rules build A from some of its non-positive subformulas in one cluster of inferences. Note that this notion only makes sense for a conclusion made only of positive formulas, since a proof is obviously focalized on any of its non-positive conclusions, using the degenerate generalized connective P[X] = X.
Theorem
A sequent 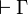 is cut-free provable if and only if it is provable
by a cut-free focalized proof.
is cut-free provable if and only if it is provable
by a cut-free focalized proof.
Proof. We reason by induction on a proof π of Γ. As noted above, the result trivially holds if Γ has a non-positive formula. We can thus assume that Γ contains only positive formulas and reason on the nature of the last rule, which is necessarily the introduction of a positive connective (it cannot be an axiom rule because an axiom always has at least on non-positive conclusion).
Suppose that the last rule of π introduces a tensor, so that π is
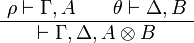
By induction hypothesis, there are focalized proofs 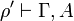 and
and 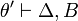 .
If A is the focus of ρ' and B is the focus of θ', then the
proof
.
If A is the focus of ρ' and B is the focus of θ', then the
proof
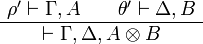
is focalized on 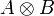 , so we can conclude.
Otherwise, one of the two proofs is focalized on another conclusion.
Without loss of generality, suppose that ρ' is not focalized on A.
Then it decomposes as
, so we can conclude.
Otherwise, one of the two proofs is focalized on another conclusion.
Without loss of generality, suppose that ρ' is not focalized on A.
Then it decomposes as
![\AxRule{ \rho_1 \vdash \Gamma_1, C_{i_1} }
\AxRule{ \cdots }
\AxRule{ \rho_\ell \vdash \Gamma_\ell, C_{i_\ell} }
\TriRule{ \vdash \Gamma_1, \ldots, \Gamma_\ell, P[C_1,\ldots,C_n] }
\DisplayProof](/mediawiki/images/math/1/4/4/144b7b5bc9f20d7e048b04acb7b10c72.png)
where the Ci are not positive and A belongs to some context Γj that we will write Γ'j,A. Then we can conclude with the proof
![\AxRule{ \rho_1 \vdash \Gamma_1, C_{i_1} \quad\cdots }
\AxRule{ \rho_j \vdash \Gamma_j, A, C_{i_j} }
\AxRule{ \theta \vdash \Delta, B }
\BinRule{ \vdash \Gamma_j, \Delta, A\tens B, C_{i_j} }
\AxRule{ \cdots\quad \rho_\ell \vdash \Gamma_\ell, C_{i_\ell} }
\TriRule{ \vdash \Gamma_1, \ldots, \Gamma_\ell, \Delta, A\tens B, P[C_1,\ldots,C_n] }
\DisplayProof](/mediawiki/images/math/b/3/6/b36a3cbfaba2b31dc22d4a21fb851203.png)
which is focalized on ![P[C_1,\ldots,C_n]](/mediawiki/images/math/e/5/5/e5568259296c6393b40172e6766e7136.png) .
.
If the last rule of π introduces a 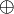 , we proceed the same way
except that there is only one premiss.
If the last rule of π introduces a
, we proceed the same way
except that there is only one premiss.
If the last rule of π introduces a 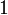 , then it is the only rule of
π, which is thus focalized on this
, then it is the only rule of
π, which is thus focalized on this 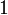 .
.
As in the reversibility theorem, this proof only makes use of commutation of independent rules.
These results say nothing about exponential modalities, because they respect neither reversibility nor focalization. However, if we consider the fragment of LL which consists only of multiplicative and additive connectives, we can restrict the proof rules to enforce focalization without loss of expressiveness.