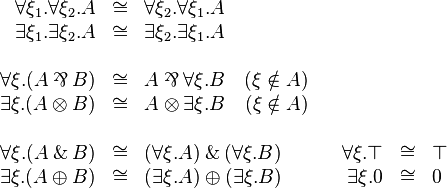List of isomorphisms

From LLWiki
(Difference between revisions)
Jump to: navigation, search
(First list)
 
(Quantifiers added)
 
Line 73: Line 73:
 
\oc(A\with B) &\cong& \oc A\tens\oc B &\quad& \oc\top &\cong& \one\\
  
\oc(A\with B) &\cong& \oc A\tens\oc B &\quad& \oc\top &\cong& \one\\
 
\wn(A\plus B) &\cong& \wn A\parr\wn B &\quad& \wn\zero &\cong& \bot\\
  
\wn(A\plus B) &\cong& \wn A\parr\wn B &\quad& \wn\zero &\cong& \bot\\
  +
\end{array}
  +
</math>
  +
  +
== Quantifiers ==
  +
  +
  +
<math>
  +
\begin{array}{rclcrcl}
  +
\forall \xi_1. \forall\xi_2. A &\cong& \forall\xi_2. \forall\xi_1. A\\
  +
\exists \xi_1. \exists\xi_2.A &\cong& \exists\xi_2.\exists\xi_1.A\\
  +
\\
  +
\forall \xi . (A \parr B) &\cong& A \parr \forall \xi.B \quad (\xi\notin A) \\
  +
\exists \xi . (A \tens B) &\cong& A \tens \exists \xi.B \quad (\xi\notin A) \\
  +
\\
  +
\forall \xi . (A \with B) &\cong& (\forall \xi . A) \with (\forall \xi . B) & & \forall \xi . \top &\cong& \top \\
  +
\exists \xi . (A \plus B) &\cong& (\exists \xi . A) \plus (\exists \xi . B) & & \exists \xi . \zero &\cong& \zero
 
\end{array}
  
\end{array}
 
</math>
  
</math>

Latest revision as of 22:43, 27 October 2013

Contents

[edit] Linear negation

\begin{array}{rclcrcl} A\biorth &\cong& A\\ (A\tens B)\orth &\cong& A\orth\parr B\orth &\quad& \one\orth &\cong& \bot\\ (A\parr B)\orth &\cong& A\orth\tens B\orth &\quad& \bot\orth &\cong& \one\\ (A\with B)\orth &\cong& A\orth\plus B\orth &\quad& \top\orth &\cong& \zero\\ (A\plus B)\orth &\cong& A\orth\with B\orth &\quad& \zero\orth &\cong& \top\\ (\oc A)\orth &\cong& \wn A\orth\\ (\wn A)\orth &\cong& \oc A\orth\\ \end{array}

[edit] Neutrals

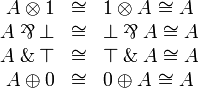
\begin{array}{rcl} A\tens\one &\cong& \one\tens A\cong A\\ A\parr\bot &\cong& \bot\parr A\cong A\\ A\with\top &\cong& \top\with A\cong A\\ A\plus\zero &\cong&\zero\plus A\cong A\\ \end{array}

[edit] Commutativity

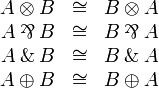
\begin{array}{rcl} A\tens B &\cong& B\tens A\\ A\parr B &\cong& B\parr A\\ A\with B &\cong& B\with A\\ A\plus B &\cong& B\plus A\\ \end{array}

[edit] Associativity

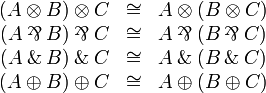
\begin{array}{rcl} (A\tens B)\tens C &\cong& A\tens(B\tens C)\\ (A\parr B)\parr C &\cong& A\parr(B\parr C)\\ (A\with B)\with C &\cong& A\with(B\with C)\\ (A\plus B)\plus C &\cong& A\plus(B\plus C)\\ \end{array}

[edit] Multiplicative-additive distributivity

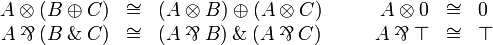
\begin{array}{rclcrcl} A\tens(B\plus C) &\cong& (A\tens B)\plus(A\tens C) &\quad& A\tens\zero &\cong& \zero\\ A\parr(B\with C) &\cong& (A\parr B)\with(A\parr C) &\quad& A\parr\top &\cong& \top\\ \end{array}

[edit] Linear implication

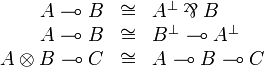
\begin{array}{rclcrcl} A\limp B &\cong& A\orth\parr B\\ A\limp B &\cong& B\orth\limp A\orth\\ A\tens B \limp C &\cong& A\limp B \limp C\\ \end{array}

[edit] The exponential isomorphisms

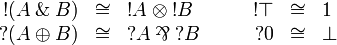
\begin{array}{rclcrcl} \oc(A\with B) &\cong& \oc A\tens\oc B &\quad& \oc\top &\cong& \one\\ \wn(A\plus B) &\cong& \wn A\parr\wn B &\quad& \wn\zero &\cong& \bot\\ \end{array}

[edit] Quantifiers

\begin{array}{rclcrcl} \forall \xi_1. \forall\xi_2. A &\cong& \forall\xi_2. \forall\xi_1. A\\ \exists \xi_1. \exists\xi_2.A &\cong& \exists\xi_2.\exists\xi_1.A\\ \\ \forall \xi . (A \parr B) &\cong& A \parr \forall \xi.B \quad (\xi\notin A) \\ \exists \xi . (A \tens B) &\cong& A \tens \exists \xi.B \quad (\xi\notin A) \\ \\ \forall \xi . (A \with B) &\cong& (\forall \xi . A) \with (\forall \xi . B) & & \forall \xi . \top &\cong& \top \\ \exists \xi . (A \plus B) &\cong& (\exists \xi . A) \plus (\exists \xi . B) & & \exists \xi . \zero &\cong& \zero \end{array}

Retrieved from "http://llwiki.ens-lyon.fr/mediawiki/index.php?title=List_of_isomorphisms&oldid=591"
Personal tools