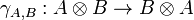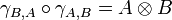Categorical semantics

Revision as of 18:16, 23 March 2009

TODO: why categories? how to extract categorical models? etc.

See ^[1]for a more detailed introduction to category theory.

A model of IMLL is a closed symmetric monoidal category. We recall the definition of these categories below.

Definition (Monoidal category)

A monoidal category $(\mathcal{C},\otimes,I)$ is a category $\mathcal{C}$ equipped with

a functor 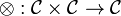$\otimes:\mathcal{C}\times\mathcal{C}\to\mathcal{C}$ called tensor product,
an object $I$ called unit object,
three natural isomorphisms of components

$\alpha_{A,B,C}:(A\otimes B)\otimes C\to A\otimes (B\otimes C) \qquad \lambda_A:I\otimes A\to A \qquad \rho_A:A\otimes I\to A$

called respectively associator, left unitor and right unitor,

such that

commutes,

commute.

Definition (Braided, symmetric monoidal category)

A braided monoidal category is a category together with a natural isomorphism of components

$\gamma_{A,B}:A\otimes B\to B\otimes A$

called braiding, such that the two diagrams

UNIQ608f0e501ac4bb45-math-0000000E-QINU

commute for every objects $A$ , $B$ and $C$ .

A symmetric monoidal category is a braided monoidal category in which the braiding satisfies

$\gamma_{B,A}\circ\gamma_{A,B}=A\otimes B$

for every objects $A$ and $B$ .

Definition (*-autonomous category)

TODO

@@ Line 38: / Line 38: @@
 :<math>\gamma_{B,A}\circ\gamma_{A,B}=A\otimes B</math>
 for every objects <math>A</math> and <math>B</math>.
+}}
+== Modeling [[IMALL]] ==
+== Modeling negation ==
+{{Definition|title=*-autonomous category|
+TODO
 }}