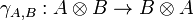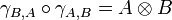Categorical semantics
From LLWiki
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
TODO: why categories? how to extract categorical models? etc. |
TODO: why categories? how to extract categorical models? etc. |
||
| − | == Categories recalled == |
||
See <ref>{{BibEntry|bibtype=book|author=MacLane, Saunders|title=Categories for the Working Mathematician|publisher=Springer Verlag,year=1971,volume=5,series=Graduate Texts in Mathematics}}</ref>for a more detailed introduction to category theory. |
See <ref>{{BibEntry|bibtype=book|author=MacLane, Saunders|title=Categories for the Working Mathematician|publisher=Springer Verlag,year=1971,volume=5,series=Graduate Texts in Mathematics}}</ref>for a more detailed introduction to category theory. |
||
| − | === Monoidal categories === |
+ | == Modeling [IMLL] == |
| + | |||
| + | A model of [IMLL] is a ''closed symmetric monoidal category''. We recall the definition of these categories below. |
||
{{Definition|title=Monoidal category| |
{{Definition|title=Monoidal category| |
||
Revision as of 18:14, 23 March 2009
TODO: why categories? how to extract categorical models? etc.
See [1]for a more detailed introduction to category theory.
Modeling [IMLL]
A model of [IMLL] is a closed symmetric monoidal category. We recall the definition of these categories below.
Definition (Monoidal category)
A monoidal category  is a category
is a category  equipped with
equipped with
- a functor
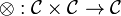 called tensor product,
called tensor product,
- an object I called unit object,
- three natural isomorphisms of components
called respectively associator, left unitor and right unitor,
such that
- for every objects A,B,C,D in
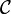 , the diagram
, the diagram
commutes,
- for every objects A and B in
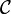 , the diagrams
, the diagrams
commute.
Definition (Braided, symmetric monoidal category)
A braided monoidal category is a category together with a natural isomorphism of components
called braiding, such that the two diagrams
- UNIQ577e81354c9fb9f2-math-0000000E-QINU
commute for every objects A, B and C.
A symmetric monoidal category is a braided monoidal category in which the braiding satisfies
for every objects A and B.
References
- ↑ MacLane, Saunders. Categories for the Working Mathematician.