Categorical semantics

From LLWiki
(Difference between revisions)
Jump to: navigation, search
(monoidal categories)
 
Line 1: Line 1:
 
TODO: why categories? how to extract categorical models? etc.
  
TODO: why categories? how to extract categorical models? etc.
  +
  +
== Categories recalled ==
  +
  +
=== Monoidal categories ===
   
 
{{Definition|title=Monoidal category|
  
{{Definition|title=Monoidal category|

Revision as of 17:57, 23 March 2009

TODO: why categories? how to extract categorical models? etc.

Categories recalled

Monoidal categories

Definition (Monoidal category)

A monoidal category 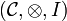(\mathcal{C},\otimes,I) is a category 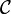\mathcal{C} equipped with

  • a functor 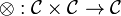\otimes:\mathcal{C}\times\mathcal{C}\to\mathcal{C} called tensor product,
  • an object I called unit object,
  • three natural isomorphisms of components
\alpha_{A,B,C}:(A\otimes B)\otimes C\to A\otimes (B\otimes C) \qquad \lambda_A:I\otimes A\to A \qquad \rho_A:A\otimes I\to A

called respectively associator, left unitor and right unitor,

such that

  • for every objects A,B,C,D in 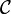\mathcal{C}, the diagram

commutes,

  • for every objects A and B in 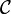\mathcal{C}, the diagrams

commute.

Retrieved from "http://llwiki.ens-lyon.fr/mediawiki/index.php?title=Categorical_semantics&oldid=284"
Personal tools