Relational semantics
(→Exponentials) |
m (Added k \in \Nat in the definition of the interpretation of a derivation whose last rule is promotion.) |
||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 5: | Line 5: | ||
=== The category of sets and relations === |
=== The category of sets and relations === |
||
| − | It is the category <math>\mathbf{Rel}</math> whose objects are sets, and such that <math>\mathbf{Rel}(X,Y)=\mathcal P(X\times Y)</math>. Composition is the ordinary composition of relations: given <math>s\in\mathbf{Rel}(X,Y)</math> and <math>t\in\mathbf{Rel}(Y,Z)</math>, one |
+ | It is the category <math>\mathbf{Rel}</math> whose objects are sets, and such that <math>\mathbf{Rel}(X,Y)=\powerset{X\times Y}</math>. Composition is the ordinary composition of relations: given <math>s\in\mathbf{Rel}(X,Y)</math> and <math>t\in\mathbf{Rel}(Y,Z)</math>, one |
sets <math>t\circ s=\set{(a,c)\in X\times Z}{\exists b\in Y\ (a,b)\in s\ \text{and}\ (b,c)\in t}</math> and the identity morphism is the diagonal relation <math>\mathsf{Id}_X=\set{(a,a)}{a\in X}</math>. |
sets <math>t\circ s=\set{(a,c)\in X\times Z}{\exists b\in Y\ (a,b)\in s\ \text{and}\ (b,c)\in t}</math> and the identity morphism is the diagonal relation <math>\mathsf{Id}_X=\set{(a,a)}{a\in X}</math>. |
||
| Line 17: | Line 17: | ||
<math>\rho_X\in\mathbf{Rel}(X\tens\one,X)</math> (left and right neutrality of <math>\one</math> for <math>\tens</math>) and <math>\alpha_{X,Y,Z}\in\mathbf{Rel}((X\tens Y)\tens Z,X\tens(Y\tens Z))</math> (associativity of <math>\tens</math>). All these isomorphisms have to satisfy a number of commutations. In the present case, they are defined in the obvious way. |
<math>\rho_X\in\mathbf{Rel}(X\tens\one,X)</math> (left and right neutrality of <math>\one</math> for <math>\tens</math>) and <math>\alpha_{X,Y,Z}\in\mathbf{Rel}((X\tens Y)\tens Z,X\tens(Y\tens Z))</math> (associativity of <math>\tens</math>). All these isomorphisms have to satisfy a number of commutations. In the present case, they are defined in the obvious way. |
||
| − | This monoidal category <math>(\mathbf{Rel},\tens,\one,\lambda,\rho)</math> is symmetric, meaning that it is endowed with an additional natural isomorphism <math>\sigma_{X,Y}\in\mathbf{Rel}(X\tens Y,Y\tens X)</math>, also subject to some commutations. Here, again, this isomorphism is defined in the obvious way (symmetry of the cartesian product). So, to be precise, the SMCC (symmetric monoidal closed category) <math>\mathbf{Rel}</math> is the tuple <math>(\mathbf{Rel},\tens,\one,\lambda,\rho,\alpha,\sigma)</math>, but we shall simply denote it as <math>\mathbf{Rel}</math> for simplicity. |
+ | This monoidal category <math>(\mathbf{Rel},\tens,\one,\lambda,\rho)</math> is symmetric, meaning that it is endowed with an additional natural isomorphism <math>\sigma_{X,Y}\in\mathbf{Rel}(X\tens Y,Y\tens X)</math>, also subject to some commutations. Here, again, this isomorphism is defined in the obvious way (symmetry of the cartesian product). So, to be precise, the SMCC (symmetric monoidal closed category) <math>\mathbf{Rel}</math> is the tuple <math>(\mathbf{Rel},\tens,\one,\lambda,\rho,\alpha,\sigma)</math>, but we shall simply denote it as <math>\mathbf{Rel}</math>. |
The SMCC <math>\mathbf{Rel}</math> is closed. This means that, given any object <math>X</math> of <math>\mathbf{Rel}</math> (a set), the functor <math>Z\mapsto Z\tens X</math> (from <math>\mathbf{Rel}</math> to <math>\mathbf{Rel}</math>) admits a right adjoint <math>Y\mapsto (X\limp Y)</math> (from <math>\mathbf{Rel}</math> to <math>\mathbf{Rel}</math>). In other words, for any objects <math>X</math> and <math>Y</math>, we are given an object <math>X\limp Y</math> and a morphism <math>\mathsf{ev}_{X,Y}\in\mathbf{Rel}((X\limp Y)\tens X,Y)</math> with the following universal property: for any morphism <math>s\in\mathbf{Rel}(Z\tens X,Y)</math>, there is a unique morphism <math>\mathsf{fun}(s)\in\mathbf{Rel}(Z,X\limp Y)</math> such that <math>\mathsf{ev}_{X,Y}\circ(\mathsf{fun}(s)\tens\mathsf{Id}_X)=s</math>. |
The SMCC <math>\mathbf{Rel}</math> is closed. This means that, given any object <math>X</math> of <math>\mathbf{Rel}</math> (a set), the functor <math>Z\mapsto Z\tens X</math> (from <math>\mathbf{Rel}</math> to <math>\mathbf{Rel}</math>) admits a right adjoint <math>Y\mapsto (X\limp Y)</math> (from <math>\mathbf{Rel}</math> to <math>\mathbf{Rel}</math>). In other words, for any objects <math>X</math> and <math>Y</math>, we are given an object <math>X\limp Y</math> and a morphism <math>\mathsf{ev}_{X,Y}\in\mathbf{Rel}((X\limp Y)\tens X,Y)</math> with the following universal property: for any morphism <math>s\in\mathbf{Rel}(Z\tens X,Y)</math>, there is a unique morphism <math>\mathsf{fun}(s)\in\mathbf{Rel}(Z,X\limp Y)</math> such that <math>\mathsf{ev}_{X,Y}\circ(\mathsf{fun}(s)\tens\mathsf{Id}_X)=s</math>. |
||
| Line 24: | Line 24: | ||
Let <math>\bot=\one=\{*\}</math>. Then we have <math>\mathsf{ev}\circ\sigma:\mathbf{Rel}(X\tens(X\limp\bot),\bot)</math> and hence <math>\eta_X=\mathsf{fun}(\mathsf{ev}\circ\sigma)\in\mathbf{Rel}(X,(X\limp\bot)\limp\bot)</math>. It is clear that <math>\eta=\set{(a,((a,*),*))}{a\in X}</math> and hence <math>\eta</math> is a natural isomorphism: one says that the SMCC <math>\mathbf{Rel}</math> is a *-autonomous category, with <math>\bot</math> as dualizing object. |
Let <math>\bot=\one=\{*\}</math>. Then we have <math>\mathsf{ev}\circ\sigma:\mathbf{Rel}(X\tens(X\limp\bot),\bot)</math> and hence <math>\eta_X=\mathsf{fun}(\mathsf{ev}\circ\sigma)\in\mathbf{Rel}(X,(X\limp\bot)\limp\bot)</math>. It is clear that <math>\eta=\set{(a,((a,*),*))}{a\in X}</math> and hence <math>\eta</math> is a natural isomorphism: one says that the SMCC <math>\mathbf{Rel}</math> is a *-autonomous category, with <math>\bot</math> as dualizing object. |
||
| + | |||
| + | ==== Additives ==== |
||
| + | |||
| + | Given a family <math>(X_i)_{i\in I}</math>, let <math>\with_{i\in I}X_i=\cup_{i\in I}\{i\}\times X_i</math>. Let <math>\pi_j\in\mathbf{Rel}(\with_{i\in I}X_i,X_j)</math> given by <math>\pi_j=\set{((j,a),a)}{a\in X_j}</math>. Then <math>(\with_{i\in I}X_i,(\pi_i)_{i\in I})</math> is the cartesian product of the <math>X_i</math>s in the category <math>\mathbf{Rel}</math>. |
||
==== Exponentials ==== |
==== Exponentials ==== |
||
| Line 30: | Line 34: | ||
* the counit, called dereliction, is the natural transformation <math>\mathsf{der}_X\in\mathbf{Rel}(\oc X,X)</math>, given by <math>\mathsf{der}_X=\set{([a],a)}{a\in X}</math> |
* the counit, called dereliction, is the natural transformation <math>\mathsf{der}_X\in\mathbf{Rel}(\oc X,X)</math>, given by <math>\mathsf{der}_X=\set{([a],a)}{a\in X}</math> |
||
* the comultiplication, called digging, is the natural transformation <math>\mathsf{digg}_X\in\mathbf{Rel}(\oc X,\oc\oc X)</math>, given by <math>\mathsf{digg}_X=\set{(m_1+\cdots+m_n,[m_1,\dots,m_n])}{n\in\mathbb N\ \text{and}\ m_1,\dots,m_n\in\oc X}</math> |
* the comultiplication, called digging, is the natural transformation <math>\mathsf{digg}_X\in\mathbf{Rel}(\oc X,\oc\oc X)</math>, given by <math>\mathsf{digg}_X=\set{(m_1+\cdots+m_n,[m_1,\dots,m_n])}{n\in\mathbb N\ \text{and}\ m_1,\dots,m_n\in\oc X}</math> |
||
| + | |||
| + | === Interpretation of propositional linear logic (<math>LL_0</math>) === |
||
| + | |||
| + | The structure described above gives rise to the following interpretation of |
||
| + | formulas and proofs of linear logic. |
||
| + | |||
| + | For all propositional variable <math>X</math>, fix a set <math>\web X</math>. |
||
| + | Then with each formula <math>A</math>, we associate a set <math>\web A</math> as follows: |
||
| + | * <math>\web{A\orth}=\web A</math>; |
||
| + | * <math>\web{A\tens B}=\web{A\parr B}=\web A\times\web B</math>; |
||
| + | * <math>\web{A\with B}=\web{A\plus B}=(\{1\}\times\web A)\cup(\{2\}\times\web B)</math>; |
||
| + | * <math>\web{\oc A}=\web{\wn A}=\finmulset{\web A}</math>. |
||
| + | |||
| + | We then interpret the proofs of <math>LL_0</math> as follows: with each proof |
||
| + | <math>\pi</math> of sequent <math>\vdash A_1,\ldots,A_n</math>, we associate a |
||
| + | subset <math>\sem\pi\subseteq\web{A_1}\times\cdots\times\web{A_n}</math>. |
||
| + | * Identity group: |
||
| + | *: <math>\sem{ |
||
| + | \LabelRule{ \rulename{axiom} } |
||
| + | \NulRule{ \vdash A\orth, A } |
||
| + | \DisplayProof}=\set{(a,a)}{a\in\web A} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, A } |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \rho }{ \vdash \Delta, A\orth } |
||
| + | \LabelRule{ \rulename{cut} } |
||
| + | \BinRule{ \vdash \Gamma, \Delta } |
||
| + | \DisplayProof} = \set{(\gamma,\delta)}{\exists a\in\web A,\ (\gamma,a)\in\sem\pi\land(\delta,a)\in\sem\rho} |
||
| + | </math> |
||
| + | * Multiplicative group: |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, A } |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \rho }{ \vdash \Delta, B } |
||
| + | \LabelRule{ \tens } |
||
| + | \BinRule{ \vdash \Gamma, \Delta, A \tens B } |
||
| + | \DisplayProof} = \set{(\gamma,\delta,a,b)}{(\gamma,a)\in\sem\pi\land(\delta,b)\in\sem\rho} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{ } |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, A, B } |
||
| + | \LabelRule{ \parr } |
||
| + | \UnaRule{ \vdash \Gamma, A \parr B } |
||
| + | \DisplayProof} = \set{(\gamma,(a,b))}{(\gamma,a,b)\in\sem\pi} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \LabelRule{ \one } |
||
| + | \NulRule{ \vdash \one } |
||
| + | \DisplayProof} = \{ * \} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma } |
||
| + | \LabelRule{ \bot } |
||
| + | \UnaRule{ \vdash \Gamma, \bot } |
||
| + | \DisplayProof} = \set{(\gamma,*)}{\gamma\in\sem\pi} |
||
| + | </math> |
||
| + | * Additive group: |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, A } |
||
| + | \LabelRule{ \plus_1 } |
||
| + | \UnaRule{ \vdash \Gamma, A \plus B } |
||
| + | \DisplayProof} = \set{(\gamma,(1,a))}{(\gamma,a)\in\sem\pi} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, B } |
||
| + | \LabelRule{ \plus_2 } |
||
| + | \UnaRule{ \vdash \Gamma, A \plus B } |
||
| + | \DisplayProof} = \set{(\gamma,(2,b))}{(\gamma,b)\in\sem\pi} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, A } |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \rho }{ \vdash \Gamma, B } |
||
| + | \LabelRule{ \with } |
||
| + | \BinRule{ \vdash \Gamma, A \with B } |
||
| + | \DisplayProof} = \set{(\gamma,(1,a))}{(\gamma,a)\in\sem\pi} \cup \set{(\gamma,(2,b))}{(\gamma,b)\in\sem\rho} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \LabelRule{ \top } |
||
| + | \NulRule{ \vdash \Gamma, \top } |
||
| + | \DisplayProof} = \emptyset |
||
| + | </math> |
||
| + | * Exponential group: |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, A } |
||
| + | \LabelRule{ d } |
||
| + | \UnaRule{ \vdash \Gamma, \wn A } |
||
| + | \DisplayProof} = \set{(\gamma,[a])}{(\gamma,a)\in\sem\pi} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma } |
||
| + | \LabelRule{ w } |
||
| + | \UnaRule{ \vdash \Gamma, \wn A } |
||
| + | \DisplayProof} = \set{(\gamma,[])}{\gamma\in\sem\pi} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \Gamma, \wn A, \wn A } |
||
| + | \LabelRule{ c } |
||
| + | \UnaRule{ \vdash \Gamma, \wn A } |
||
| + | \DisplayProof} = \set{(\gamma,m+n)}{(\gamma,m,n)\in\sem\pi} |
||
| + | </math> |
||
| + | *: <math> |
||
| + | \sem{ |
||
| + | \AxRule{} |
||
| + | \VdotsRule{ \pi }{ \vdash \wn A_1,\ldots,\wn A_n,B } |
||
| + | \LabelRule{ \oc } |
||
| + | \UnaRule{ \vdash \wn A_1,\ldots,\wn A_n,\oc B } |
||
| + | \DisplayProof} = \set{ |
||
| + | \left(\sum_{i=1}^k m_1^i,\ldots,\sum_{i=1}^k m_n^i,[b_1,\ldots,b_k]\right)} |
||
| + | {k \in \mathbb{N} \ \text{and} \ \forall 1 \leq i \leq k,\ (m_1^i,\ldots,m_n^i,b_i)\in\sem\pi} |
||
| + | </math> |
||
| + | |||
| + | {{Theorem|If proof <math>\pi'</math> is obtained from <math>\pi</math> by eliminating a cut, |
||
| + | then <math>\sem\pi=\sem{\pi'}</math>.}} |
||
Latest revision as of 15:28, 8 February 2023
Contents |
[edit] Relational semantics
This is the simplest denotational semantics of linear logic. It consists in interpreting a formula A as a set A * and a proof π of A as a subset π * of A * .
[edit] The category of sets and relations
It is the category 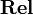 whose objects are sets, and such that
whose objects are sets, and such that 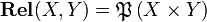 . Composition is the ordinary composition of relations: given
. Composition is the ordinary composition of relations: given 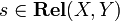 and
and 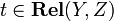 , one
sets
, one
sets 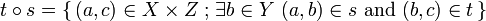 and the identity morphism is the diagonal relation
and the identity morphism is the diagonal relation 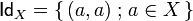 .
.
An isomorphism in the category  is a relation which is a bijection, as easily checked.
is a relation which is a bijection, as easily checked.
[edit] Monoidal structure
The tensor product is the usual cartesian product of sets  (which is not a cartesian product in the category
(which is not a cartesian product in the category 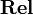 in the categorical sense). It is a bifunctor: given
in the categorical sense). It is a bifunctor: given 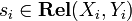 (for i = 1,2), one sets
(for i = 1,2), one sets 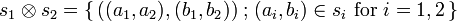 . The unit of this tensor product is
. The unit of this tensor product is 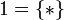 where * is an arbitrary element.
where * is an arbitrary element.
For defining a monoidal category, it is not sufficient to provide the definition of the tensor product functor  and its unit
and its unit 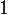 , one has also to provide natural isomorphisms
, one has also to provide natural isomorphisms 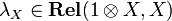 ,
,
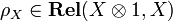 (left and right neutrality of
(left and right neutrality of 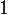 for
for  ) and
) and 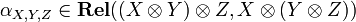 (associativity of
(associativity of  ). All these isomorphisms have to satisfy a number of commutations. In the present case, they are defined in the obvious way.
). All these isomorphisms have to satisfy a number of commutations. In the present case, they are defined in the obvious way.
This monoidal category 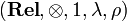 is symmetric, meaning that it is endowed with an additional natural isomorphism
is symmetric, meaning that it is endowed with an additional natural isomorphism 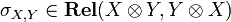 , also subject to some commutations. Here, again, this isomorphism is defined in the obvious way (symmetry of the cartesian product). So, to be precise, the SMCC (symmetric monoidal closed category)
, also subject to some commutations. Here, again, this isomorphism is defined in the obvious way (symmetry of the cartesian product). So, to be precise, the SMCC (symmetric monoidal closed category) 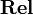 is the tuple
is the tuple 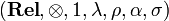 , but we shall simply denote it as
, but we shall simply denote it as 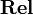 .
.
The SMCC 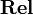 is closed. This means that, given any object X of
is closed. This means that, given any object X of 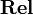 (a set), the functor
(a set), the functor 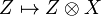 (from
(from 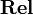 to
to 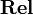 ) admits a right adjoint
) admits a right adjoint 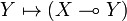 (from
(from 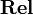 to
to 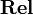 ). In other words, for any objects X and Y, we are given an object
). In other words, for any objects X and Y, we are given an object 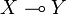 and a morphism
and a morphism 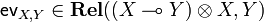 with the following universal property: for any morphism
with the following universal property: for any morphism 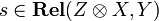 , there is a unique morphism
, there is a unique morphism 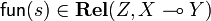 such that
such that 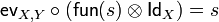 .
.
The definition of all these data is quite simple in  :
:  ,
, 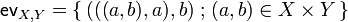 and
and 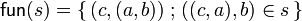 .
.
Let 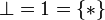 . Then we have
. Then we have 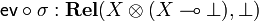 and hence
and hence 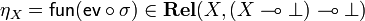 . It is clear that
. It is clear that 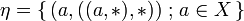 and hence η is a natural isomorphism: one says that the SMCC
and hence η is a natural isomorphism: one says that the SMCC 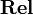 is a *-autonomous category, with
is a *-autonomous category, with 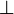 as dualizing object.
as dualizing object.
[edit] Additives
Given a family 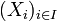 , let
, let 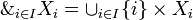 . Let
. Let 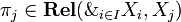 given by
given by 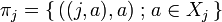 . Then
. Then 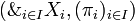 is the cartesian product of the Xis in the category
is the cartesian product of the Xis in the category 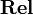 .
.
[edit] Exponentials
One defines 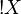 as the set of all finite multisets of elements of X. Given
as the set of all finite multisets of elements of X. Given 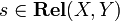 , one defines
, one defines ![\oc s=\set{([a_1,\dots,a_n],[b_1,\dots,b_n])}{n\in\mathbb N\ \text{and}\ \forall i\ (a_i,b_i)\in s}](/mediawiki/images/math/c/e/3/ce325e0d5338d3b230c6c9b8080230d4.png) where
where ![[a_1,\dots,a_n]](/mediawiki/images/math/6/6/4/664d4579222deb590b5a7949e0ed6dce.png) is the multiset containing
is the multiset containing 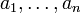 , taking multiplicities into account. This defines a functor
, taking multiplicities into account. This defines a functor 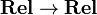 , that we endow with a comonad structure as follows:
, that we endow with a comonad structure as follows:
- the counit, called dereliction, is the natural transformation
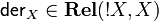 , given by
, given by ![\mathsf{der}_X=\set{([a],a)}{a\in X}](/mediawiki/images/math/d/7/8/d78030716c6bab7593eaea545f8d7e45.png)
- the comultiplication, called digging, is the natural transformation
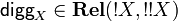 , given by
, given by ![\mathsf{digg}_X=\set{(m_1+\cdots+m_n,[m_1,\dots,m_n])}{n\in\mathbb N\ \text{and}\ m_1,\dots,m_n\in\oc X}](/mediawiki/images/math/9/9/8/9985d116af5e40da029c845b79521d16.png)
[edit] Interpretation of propositional linear logic (LL0)
The structure described above gives rise to the following interpretation of formulas and proofs of linear logic.
For all propositional variable X, fix a set 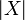 .
Then with each formula A, we associate a set
.
Then with each formula A, we associate a set 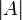 as follows:
as follows:
-
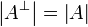 ;
;
-
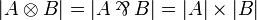 ;
;
-
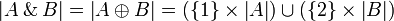 ;
;
-
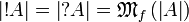 .
.
We then interpret the proofs of LL0 as follows: with each proof
π of sequent 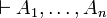 , we associate a
subset
, we associate a
subset 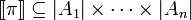 .
.
- Identity group:
-
- Multiplicative group:
-
- Additive group:
-
- Exponential group:
-
Theorem
If proof π' is obtained from π by eliminating a cut,
then 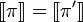 .
.
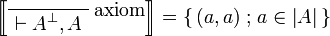
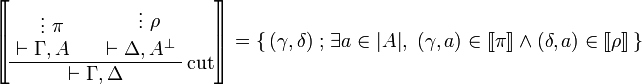
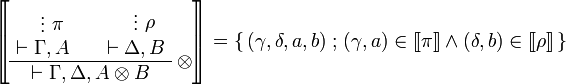
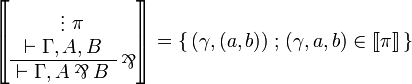
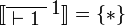
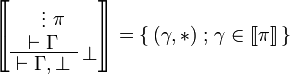
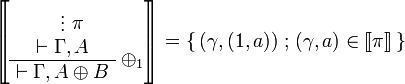
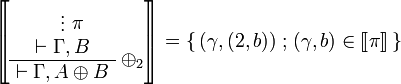
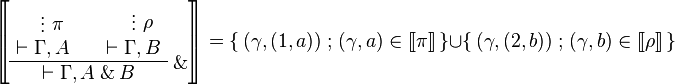
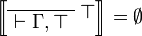
![\sem{
\AxRule{}
\VdotsRule{ \pi }{ \vdash \Gamma, A }
\LabelRule{ d }
\UnaRule{ \vdash \Gamma, \wn A }
\DisplayProof} = \set{(\gamma,[a])}{(\gamma,a)\in\sem\pi}](/mediawiki/images/math/a/2/1/a219c547538d8f2211e6ec2f9173a63b.png)
![\sem{
\AxRule{}
\VdotsRule{ \pi }{ \vdash \Gamma }
\LabelRule{ w }
\UnaRule{ \vdash \Gamma, \wn A }
\DisplayProof} = \set{(\gamma,[])}{\gamma\in\sem\pi}](/mediawiki/images/math/1/7/8/178859b80c15d7ba2ce7127bb3e10b9c.png)
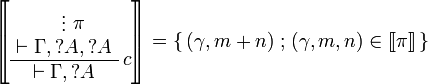
![\sem{
\AxRule{}
\VdotsRule{ \pi }{ \vdash \wn A_1,\ldots,\wn A_n,B }
\LabelRule{ \oc }
\UnaRule{ \vdash \wn A_1,\ldots,\wn A_n,\oc B }
\DisplayProof} = \set{
\left(\sum_{i=1}^k m_1^i,\ldots,\sum_{i=1}^k m_n^i,[b_1,\ldots,b_k]\right)}
{k \in \mathbb{N} \ \text{and} \ \forall 1 \leq i \leq k,\ (m_1^i,\ldots,m_n^i,b_i)\in\sem\pi}](/mediawiki/images/math/8/c/7/8c7149804b64a2d071adc7ecd21d6266.png)