Translations of intuitionistic logic
The genesis of linear logic comes with a decomposition of the intuitionistic implication. Once linear logic properly defined, it corresponds to a translation of intuitionistic logic into linear logic, often called Girard's translation. In fact Jean-Yves Girard has defined two translations in his linear logic paper[1]. We call them the call-by-name translation and the call-by-value translation.
These translations can be extended to translations of classical logic into linear logic.
Contents |
Call-by-name Girard's translation 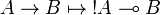
Formulas are translated as:
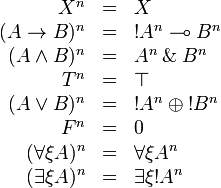
This is extended to sequents by 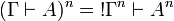 .
.
This allows one to translate the rules of intuitionistic logic into linear logic:
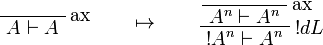
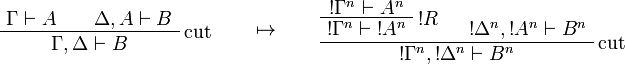
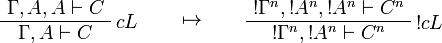
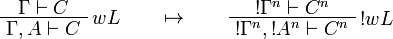
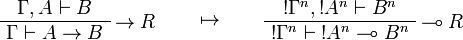
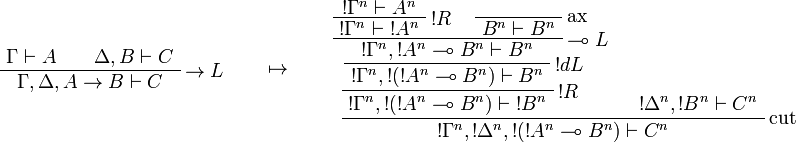
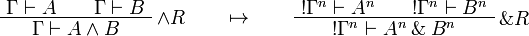
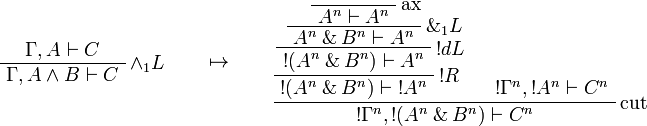
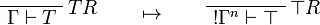
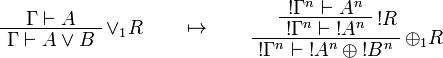
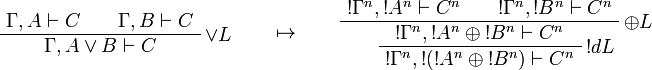
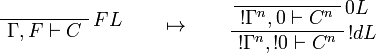
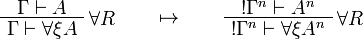
![\AxRule{\Gamma,A[\tau/\xi]\vdash C}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\xi A\vdash C}
\DisplayProof
\qquad\mapsto\qquad
\LabelRule{\rulename{ax}}
\NulRule{A^n[\tau^n/\xi]\vdash A^n[\tau^n/\xi]}
\LabelRule{\forall L}
\UnaRule{\forall\xi A^n\vdash A^n[\tau^n/\xi]}
\LabelRule{\oc d L}
\UnaRule{\oc{\forall\xi A^n}\vdash A^n[\tau^n/\xi]}
\LabelRule{\oc R}
\UnaRule{\oc{\forall\xi A^n}\vdash \oc{(A^n[\tau^n/\xi])}}
\AxRule{\oc{\Gamma^n},\oc{(A^n[\tau^n/\xi])}\vdash C^n}
\LabelRule{\rulename{cut}}
\BinRule{\oc{\Gamma^n},\oc{\forall\xi A^n}\vdash C^n}
\DisplayProof](/mediawiki/images/math/d/5/c/d5cee7e0d3193ed8f5cfe81c35383ad8.png)
![\AxRule{\Gamma\vdash A[\tau/\xi]}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash \exists\xi A}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\oc{\Gamma^n}\vdash A^n[\tau^n/\xi]}
\LabelRule{\oc R}
\UnaRule{\oc{\Gamma^n}\vdash \oc{(A^n[\tau^n/\xi])}}
\LabelRule{\exists R}
\UnaRule{\oc{\Gamma^n}\vdash \exists\xi\oc{A^n}}
\DisplayProof](/mediawiki/images/math/1/a/f/1af8899204390f21703fe4649ca8ff4b.png)
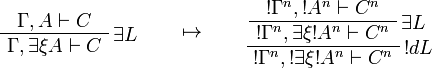
Call-by-value translation 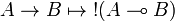
Formulas are translated as:
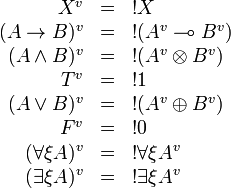
The translation of any formula starts with 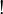 , we define
, we define 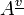 such that
such that 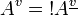 .
.
The translation of sequents is 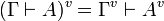 .
.
This allows one to translate the rules of intuitionistic logic into linear logic:
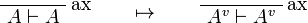
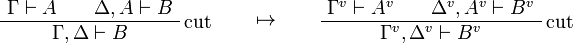
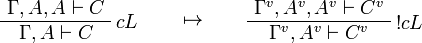
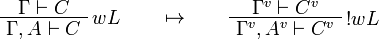
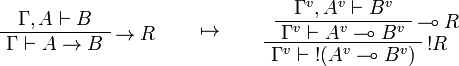
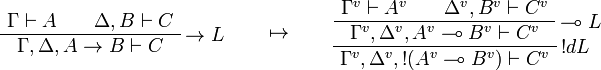
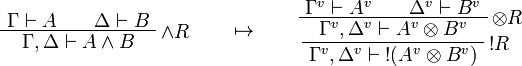
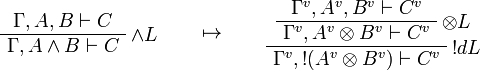
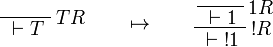
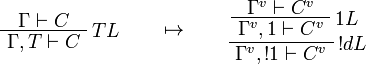
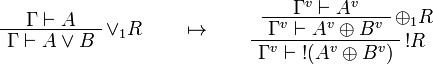
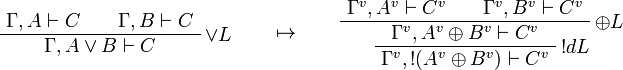
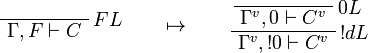
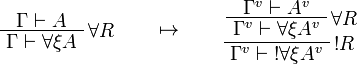
We use ![(A[\tau/\xi])^v=A^v[\tau^{\underline{v}}/\xi]](/mediawiki/images/math/a/9/d/a9d5b23683d35f64287bdbea06658fbe.png) .
.
![\AxRule{\Gamma,A[\tau/\xi]\vdash C}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\xi A\vdash C}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\Gamma^v,A^v[\tau^{\underline{v}}/\xi]\vdash C^v}
\LabelRule{\forall L}
\UnaRule{\Gamma^v,\forall\xi A^v\vdash C^v}
\LabelRule{\oc d L}
\UnaRule{\Gamma^v,\oc{\forall\xi A^v}\vdash C^v}
\DisplayProof](/mediawiki/images/math/9/b/9/9b9ebf1ad781ab0f8b9de449371f9956.png)
![\AxRule{\Gamma\vdash A[\tau/\xi]}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash \exists\xi A}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\Gamma^v\vdash A^v[\tau^{\underline{v}}/\xi]}
\LabelRule{\exists R}
\UnaRule{\Gamma^v\vdash \exists\xi A^v}
\LabelRule{\oc R}
\UnaRule{\Gamma^v\vdash \oc{\exists\xi A^v}}
\DisplayProof](/mediawiki/images/math/9/9/b/99b9160fe495dd287fe79cde394069c2.png)
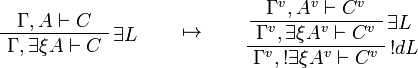
Alternative presentation
It is also possible to define 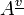 as the primitive construction.
as the primitive construction.
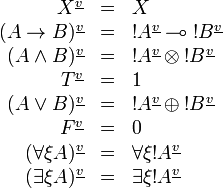
If we define 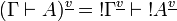 , we have
, we have 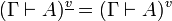 and thus we obtain the same translation of proofs.
and thus we obtain the same translation of proofs.
Call-by-value Girard's translation 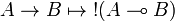
The original version of the call-by-value translation given by Jean-Yves Girard[1] is an optimisation of the previous one using properties of positive formulas.
Formulas are translated as:
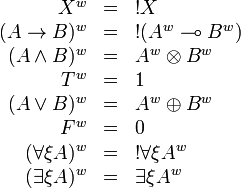
The translation of any formula is a positive formula.
The translation of sequents is 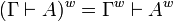 .
.
This allows one to translate the rules of intuitionistic logic into linear logic:
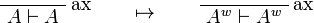
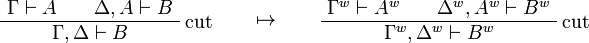

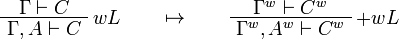
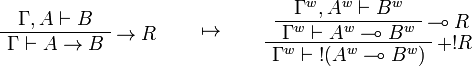
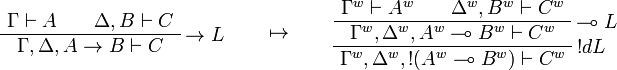
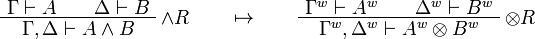
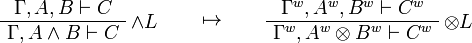
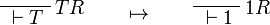
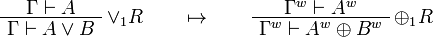
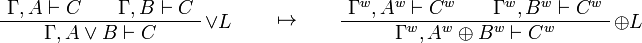
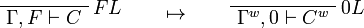
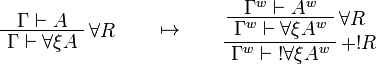
We use ![(A[\tau/\xi])^w\linequiv A^w[\tau^w/\xi]](/mediawiki/images/math/1/f/e/1fed7f14b8b6a3f49aca3fb9279ea6a1.png) .
.
![\AxRule{\Gamma,A[\tau/\xi]\vdash C}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\xi A\vdash C}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\Gamma^w,(A[\tau/\xi])^w\vdash C^w}
\UnaRule{\Gamma^w,A^w[\tau^w/\xi]\vdash C^w}
\LabelRule{\forall L}
\UnaRule{\Gamma^w,\forall\xi A^w\vdash C^w}
\LabelRule{\oc d L}
\UnaRule{\Gamma^w,\oc{\forall\xi A^w}\vdash C^w}
\DisplayProof](/mediawiki/images/math/2/3/2/232545bcbc0fbcc7465d3ed9f750a42b.png)
![\AxRule{\Gamma\vdash A[\tau/\xi]}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash \exists\xi A}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\Gamma^w\vdash (A[\tau/\xi])^w}
\UnaRule{\Gamma^w\vdash A^w[\tau^w/\xi]}
\LabelRule{\exists R}
\UnaRule{\Gamma^w\vdash \exists\xi A^w}
\DisplayProof](/mediawiki/images/math/e/f/c/efc024440beb68a1b97abf848815394e.png)
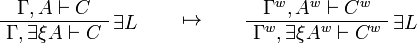
References
- ↑ 1.0 1.1 Girard, Jean-Yves. Linear logic. Theoretical Computer Science. Volume 50, Issue 1, pp. 1-101, doi:10.1016/0304-3975(87)90045-4, 1987.