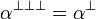Orthogonality relation
From LLWiki
Orthogonality relations are used pervasively throughout linear logic models, being often used to define somehow the duality operator 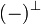 .
.
Definition (Orthogonality relation)
Let A and B be two sets. An orthogonality relation on A and B is a binary relation 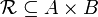 . We say that
. We say that 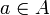 and
and 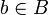 are orthogonal, and we note
are orthogonal, and we note 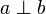 , whenever
, whenever 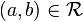 .
.
Let us now assume an orthogonality relation over A and B.
Definition (Orthogonal sets)
Let 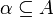 . We define its orthogonal set
. We define its orthogonal set 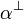 as
as 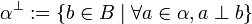 .
.
Symmetrically, for any 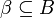 , we define
, we define 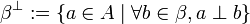 .
.
Orthogonal sets define Galois connections and share many common properties.
Proposition
For any sets 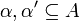 :
:
-
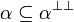
- If
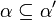 , then
, then 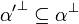
-